Bayesian ANOVA in JASP - how does it work?

Flaihai

Hi everyone,

my name is Jan and I'm currently working on my Bachelor's thesis. My task is to replicate a study. In the original study, four group means were analysed by an ANOVA with the hypothesis, that the means would not show any differences (i.e. the groups means being comparable). In a private mail, the authors stated that they didn't focus on NHST but simply analysed the data "in a loose way" by comparing means for each item.

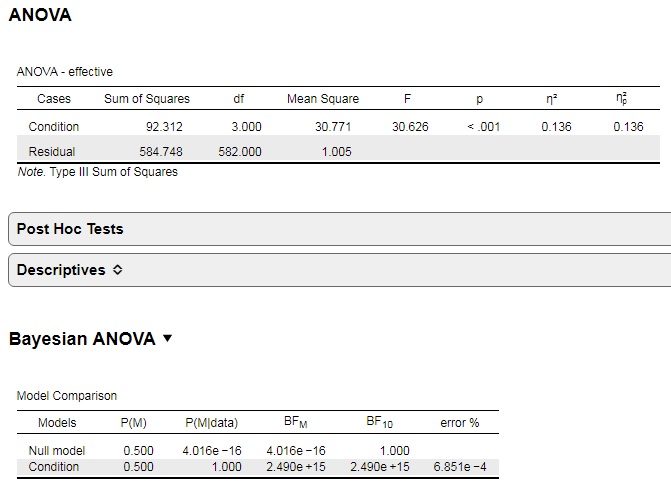
Now, for the replication, I have identified an item which did show quite a statistically significant difference and effect size (see attached file) - so it seems suitable for a replication project. To determine, whether there actually exists a difference between groups, I'd like to use Bayes factors.

Now, here are my questions:

1) I wish to calculate the BF by hand from the rregular ANOVA output. Using the equation provided by Wagenmakers et al. (2007) I first calculate deltaBIC10 = n*ln(SSError/(SSError+SSEffect))+ (k1-k0)*ln n

So far, after consulting further literature, I still do not understand, what value to insert for k1 and k0 in my case. And what is the underlying routine in JASP for the BAYES ANOVA/Bayes factor calculation?

2) Running the Bayesian ANOVA in JASP for that item with the statistically significant differences and the large effect size, results in a Bayes Factor10 of 2.49e+15

Is this a plausible result?

Thank you for your much appreciated hints and help,

Jan Krebs

EJ

Hi Jan,

1. The effect is massive, so it is a plausible result;
2. The ANOVA routine in JASP is taken from the BayesFactor package. What this package does is explained in a paper by Rouder et al. 2012 (Journal of Mathematical Psychology) and this one: http://www.ejwagenmakers.com/2017/RouderEtAl2017ANOVAPM.pdf Basically, it is a less rough version of BIC.
3. The difference between k1 and k2 is the difference is the number of free parameter between H0 en H1. If I had to guess (and I'm doing this on the spot now), with four groups the H0 has one parameter (the grand mean, which is the same for all groups) and H1 has four parameters (the grand mean and 3 differences -- the fourth difference one follows from these). Anyway, I would use the ANOVA in JASP instead of BIC.

E.J.

Flaihai

Thank you so much, E. J., for your very quick, effective and much appreciated help!

Since JASP and Bayes factors still seem to be not as recognised and famous as they maybe should, it seems almost too easy to just report the JASP output in my thesis.

I'd stil love to get at least comparable results using the manual way to report them along with JASP. When I plug in the numbers of the ANOVA into the equation 14 of your 2007 study (A pracitcal solution...), it looks like this:

deltaBIC10 = 586*ln((584.7/584.7+92.3))+3*ln 586 = -67.62

BF01 = e^(-67.62/2) = 2.07^-15

BF10 = 1/2.07^-15 = 54898

This is quite a difference to the BF10 calculated by JASP (BF10 = 876981)

Shouldn't be those results be at least close and not this different?

I'd love to hear from you on this.

Best,

Jan

EJ

Hi Jan,

I don't think this is a difference that affects the conclusion, both BF are astronomical :-)

Cheers,

E.J.