Help with the JASP Likelihood Function (MATLAB)
Hi all, I am trying to implement the JZS/objective approach to calculating Bayes Factors (the approach used in JASP and the R BayesFactor package) in Matlab, with a view toward creating a power analysis toolkit. Although I am close, the BFs I calculate are slightly off compared to JASP and the PCL web tool.
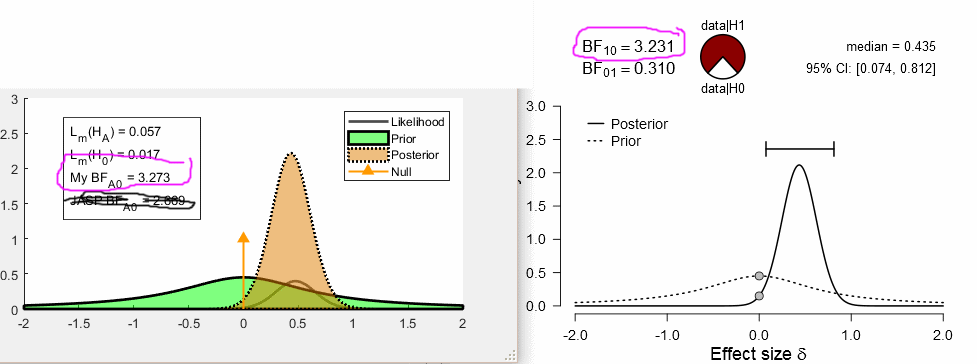
I understand the objective prior, and my implementation looks identical to that in JASP. But I'm not clear on the Likelihood function, and the likelihood I calculate appears different from what appears in JASP. I have tried a few but here was my closest:
sample.likelihood =
@(delta) tpdf( (sample.mean - (delta * sample.se * sqrt(sample.n)) ) / sample.se, sample.n-1);
JASP doesn't provide any likelihood info, and the R code may as well be hieroglyphics for as clear as it is to me. So I can really only judge by comparing the graphs in JASP to the ones I produce (example below). It appears that my prior matches but the posterior is slightly taller and narrower, presumably because of the likelihood calculation.
So, is my likelihood calculation off? Thanks if anyone can help.
By the way, probably aggravating this confusion is that I'm not clear what the x axis represents in this analysis (labelled as "Effect Size delta"). Am I correct in thinking this is Cohen's d? But we use t distributions so I get confused whether it is related to the_ t _stat or the delta parameter from a noncentral t distribution.







Comments
Hi MattO,
You might want to check out this paper: http://www.ejwagenmakers.com/2016/LyEtAl2016JMP.pdf
Effect size delta is defined as mu/sigma.
As an aside, I was a MATLAB user myself, a bunch of my friends use MATLAB, but I have to say that the closed-source aspect of it has started to rub me the wrong way in recent years. Isn't Octave an open-source version? A was recently sent a .mat file and it was basically useless to me.
Cheers,
E.J.
Thanks EJ, it looks like Equation 8 is the likelihood function I have been looking for. (Is Equation 9 the marginal likelihood?) I had not realized that I needed sigma in the likelihood function too.
I have implemented it and get still different BFs values than before, but still close. I'm not sure if perhaps it has something to do with the integral function in MATLAB. I also don't know if it's specific calculation problem with the marginal likelihood of the alternative, or of the null. If there are any other sources that provide the marginals you could recommend, it would help me to isolate the issue.
Thanks,
Matt
You can also implement this in WinBUGS and use Savage-Dickey (the Wetzels et al. 2011 PBR approach), or use Stan and the bridgesampling package.
E.J.