ESs and Credible Intervals for One vs Two Sided Bayesian t-Tests
Dear colleagues.
I’m looking for a bit of advice on reporting ES delta and its 95% credible interval in the context of a one-sided Bayesian t-test computed in JASP.
The figure below is the posterior distribution of ES delta under a default one sided prior distribution. A one sided prior was used as the relevant hypothesis was theoretically derived and directional.The BF is non-diagnostic. This is fine (as they say, data don't care what your hypotheses are), and not the issue that I'm concerned about. The median of the posterior distribution is .17, and its 95% credible interval grazes zero (but can’t extend below it).
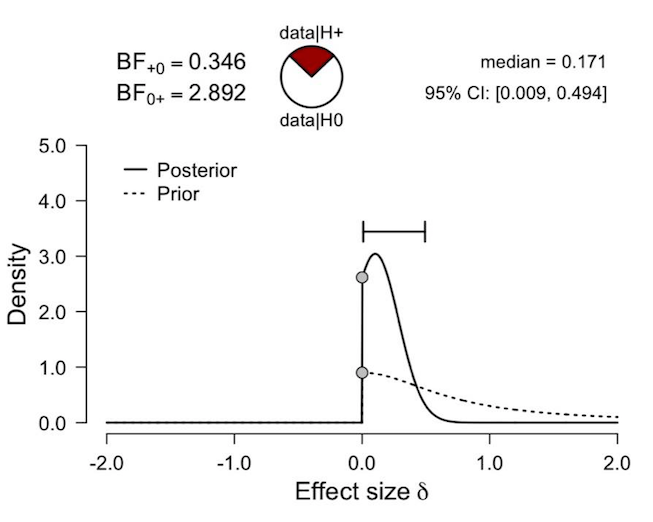
Should I report the above ES and the corresponding credible interval?
Or should I re-run the analyses with a two sided prior (see below), ignore the BF, but report ES delta = .10, 95% Credible Interval [-.27, .47]? If so, how should I explain this in the manuscript?
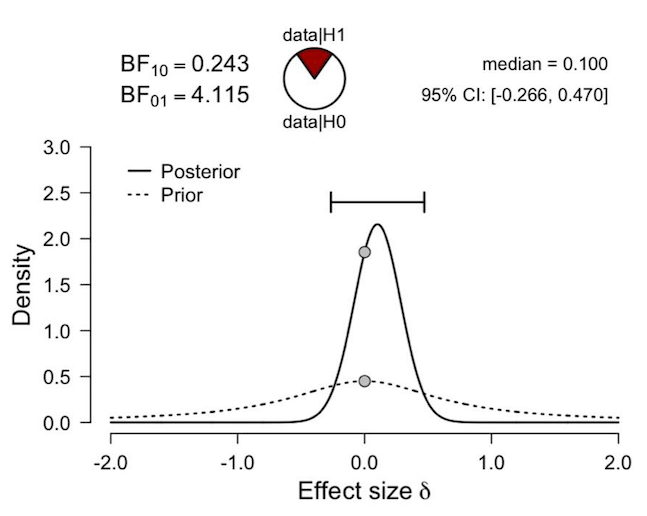
The latter (report and interpret the one sided BF followed by two sided ES and credible interval) appears to be the approach that Wagenmakers et al. (2016) have taken here, in a context which is pretty similar to the one that I am in currently: https://frontiersin.org/articles/10.3389/fpsyg.2015.00494/full. However, this seems inconsistent to me for reasons I can’t articulate. Is anyone able to explain to me why this is the sensible thing to do (or not)?
Thanks in advance for any and all advice received. I’m quite new to this Bayesian business, and still very much a novice. Peter Allen







Comments
Dear Peter,
Sorry for the tardy reply. Let me explain my reasoning. In early work, we would specify a directional hypothesis and use that both for BFs and for effect sizes. This is consistent and sensible. So why have we started to use a two-sided prior for ES? There are several reasons but one of them is that for a one-sided ES people might say: "ah, the effect is small but the central 95% interval does not overlap with zero". Of course this has to happen because of the restriction, but this is what people will quickly forget. So for ES we use the two-sided analysis (which is also similar to the classical way of doing things) but for the BF, which depends on predictive adequacy, we do respect the directional nature of the prior. But I completely accept that there are different ways of doing this.
Cheers,
E.J.
Hi E.J. No problem at all! Now that I've had time to think about it, your approach does make a lot of sense, and it is one that I will be adopting in my research. Thanks again. Peter Allen
hello, I would like to ask about BF10 and credible interval for two-sided ttest, this is my result, the H1 was supported, i would like to confim (a) should i report the median together with the 95% CI, (b) what does these mean, it seems they are not mean difference? (c) is it normal that F10 is positive but CI is negative?
i look forward to your reply, thanks a lot!!
(a) the median and 95% CI indicate the strength of the effect, assuming H1 is the best model.
(b) they summarize the posterior distribution (i.e., the Bayesian estimate) for standardized effect size, which is mu/sigma (i.e., the population version of Cohen's d).
(c) the fact that the CI is on negative values is just how the subtraction is done. If you change the order in which the variables are entered the distribution should reflect around 0. So it is just whether you do C1 - C2 or C2 - C1. Since you do a two-sided test, the BF does not care about the direction -- it just quantifies the evidence for the effect being not zero.
E.J.
Hi E.J., thanks a lot for your prompt reply, I got a much clear understanding on these concepts. But I still have another two questions to confirm, although I have referred to the guideline.
(a) does the 95% credible interval (CI) excluding zero could say that the data support the H1/H0? it seems similar to the confidence interval and p value in the frequentist approach, although the Bayesian estimates mean sth differently and give probabilistic interpretations.
(b) Bayesian approach quantify evidence for both alternative and null hypotheses, but if I focus on a two-sided ttest and would like a difference between conditions (H1), does it mean that 1<= BF10 < 3 and BF10<0.33 (H0 is supported) are both meaningless to me?
I look forward to your reply, thank you very much!
(a) No, but this is a popular misconception. We address it in this paper: https://psyarxiv.com/rqnu5
(b) In principle, even when you do estimation you can still take into account the fact that H0 is in play (see for instance https://journals.sagepub.com/doi/full/10.1177/2515245921992035). However, Jeffreys for instance recommended that you consider the estimation question ("how large is the difference") only after you have conclusively answered the testing question ("the difference is non-zero"). So if you don't find compelling evidence against H0 there is little reason to do estimation.