agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games







Comments
BF_m quantifies the change from prior odds to posterior odds.
Here I'd select "compare to best model" and then BF_01 for display, and you'll see how many times better the "openness" only model predicts the data compared to other models.
Cheers,
E.J.
Hello JASPers,
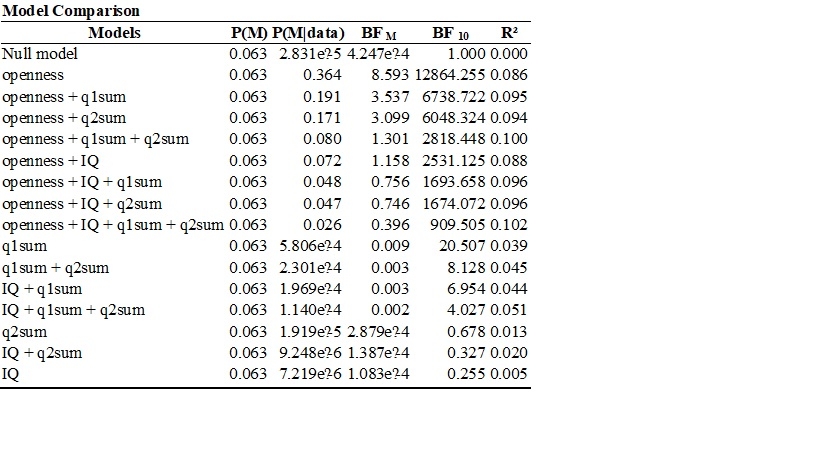
I am trying to understand how to compute the values in the Bayesian anova table below. I understand that P(M) means that the prior probabilities of the five models are equal and are obtained by 1/5. I also understand that P(M|data) refers to the posterior probability of each model after seeing the data. I also understand that BF M compares each model to the average P(M|data) of the other models. For example, the BF M of the DENSITY + SEASON Model can be obtained by 0.729/ (1- 0.729/4) = 0.729/ (0.271/4) = 0.729/0.06775 = 10.76. What I am trying to understand is how to obtain the values in BF 01. I selected BF 01 and Compare to best model and the Bayesian ANOVA table is shown below. Thanks in advance.
Cheers,
narcilili
hi again,
I think I got it regarding my question earlier today. I used the P(M|data) of the best model which is density + season as the numerator and the P(M|data) of the other models as the denominator. so, to compute BF01 for density + season + density*season I divided 0.729 by 0.251 yielding 2.9. but, dividing 0.729 by .001 yielded 729 instead of 576.852 when comparing the best model to the null model. maybe it is an approximation error?
cheers,
narcilili
Dear Narcilili,
Yes, that's an approximation error. Note that your method works because the prior model probabilities are uniform. In general, the BF column compares the model in the top row ("0") to each of the models in the rows below ("1"). You selected "best model on top", so on the first row it is compared to itself, which yields BF=1 regardless of the data. The second row shows the BF in favor of the top-row model over the model in the second row (as BF_01, because that's what you selected). So the data are 2.9 times more likely under the two-main effect model than under the model that also includes the interaction.
Cheers,
E.J.
Dear E.J.,
Thank you for your clear explanation. I would like to ask if it is possible to use Bayesian JASP for a randomized complete block design for two way ANOVA? Or an RCBD split-plot two way ANOVA? I would like to convince some agriculturists to use Baye's Factors. Thanks.
Cheers,
Narcilili
Dear Narcilili,
Hmm I have not given this much thought. Perhaps the authors of the BayesFactor package have done this, and I will attend them to this question.
Cheers,
E.J.