agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games
![]() in the design as 'nuisance', factor A is then supported (e.g. BF10 = 6.15). The factor I'm labeling as nuisance here is of less interest than factor A, but it isn't of zero interest, so I'm not sure if and when its appropriate to do so.
in the design as 'nuisance', factor A is then supported (e.g. BF10 = 6.15). The factor I'm labeling as nuisance here is of less interest than factor A, but it isn't of zero interest, so I'm not sure if and when its appropriate to do so. 






Comments
Hi R_A,
thanks for that question. It has me scratching my head. Perhaps Richard knows more. Let me look into this and get back to you.
Cheers.
E.J.
OK, after talking to Richard it is now clear to me. Consider a situation with factors A and B. BTW, a specific example is always appreciated -- note that you can upload annotated .jasp files to the OSF and everybody can view the output.
Anyway, consider the original analysis where nothing is nuisance. You have a BF10 for A+B over the null (the two main effects model; BF10(A+B)) and you have a BF10 for B over the null, BF10(B). Let's use transitivity to compute the evidence for "adding A with B already in hand": BF10(A+B)/BF10(B).
If you tick "B" as nuisance, you are comparing the "null model with B in hand" to a model that adds A. The number you get should be identical to one you get from the computation outlined above that did not involve ticking B as nuisance (the BF10(A+B)/BF10(B) operation).
You are right that BF10(A) [where you look at the support for adding A over having nothing] is not the same as BF10(A+B)/BF10(B) [where you look at the support for adding A with B in hand]. This is what it is -- maybe Richard can say more.
Of course you may wonder what analysis to report. There's at least three options: (1) be transparent and report all comparisons; (2) include the factors for which there is good support, and then see whether the factor of interest adds more -- so if there is good support for including B, include it first and then look at the support for adding A as well; (3) do an "effects" analysis where you don't focus on specific models but you average across all of them to identify the overall inclusion probability for the factor of interest.
Cheers,
E.J.
Thanks for the quick and helpful response! I did try both the transitive and nuisance approaches and they give very similar outputs, as you say. I'll try to upload the output image from the basic analysis if that will help others. The prior discussion I'd seen concerning interpretation of main effect outputs tended to imply that we just take the BF10 for each factor, when in fact the genuine BF could be being obscured by other factors in the design, as seems to be the case here.
On a general note, I am finding JASP useful and easy to use so far. My main issues have been with output interpretation (though this is proving useful in learning about the underlying mechanics). I have also had an issue with the slight variation in outputs that JASP gives between running the same analysis on the same data multiple times, but there are approaches to dealing with this. Are there any plans to expand the guidance/help sections directly associated with JASP, in order to help relative beginners overcome such bumps?
Cheers, RA.
And with Factor B labelled as nuisance...
Hi RA,
I am working on a JASP manual, and on a JASP article that describes how to interpret the JASP output for ANOVA designs. You can also check out the ANOVA paper on my website, http://www.ejwagenmakers.com/inpress/RouderEtAlinpressANOVAPM.pdf
Cheers,
E.J.
Hi,
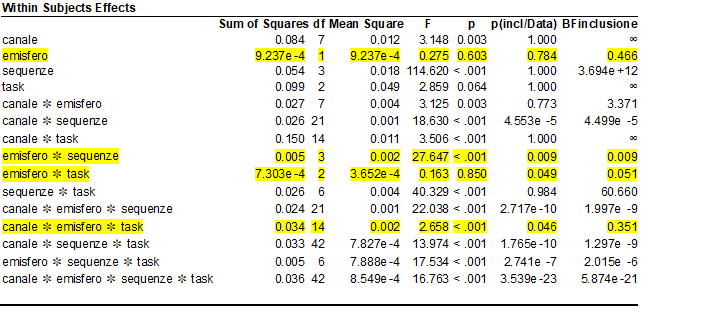
I analyzed my data with RM anova using SPSS (I have 4 RMfactors : Canale (8 levels) , Emisfero (2 levels), Sequenza(4 levels) and Task( 3 levels)
after revision the reviewer said "....the authors should then run Bayesian statistics to show that the null hypothesis is indeed true"
I tried to use JASP bayesian RM anova , the table reports RManova results and BF inclusion
Could someone help me to interpret the BF inclusion?
The BF inclusion averages across all models under consideration. It looks at all models that include the factor of interest, and pits them against all models that exclude that factor. You then look at the change from prior inclusion odds (summed prior probability for all models that include the factor versus summed prior probability for all models that exclude the factor) to posterior inclusion odds. This is the inclusion BF. The topic was discussed on the Forum several times, so when you look for it you will find more information.
Cheers,
E.J.
Thank you very much
best
Vins
Hi EJ,
the estimated Bayes inclusion factor for the effect of "task" indicated that the data were infinite times in favour of the alternative hypothesis (relative to all alternative models)... is it correct?
Hi ,
I have run bayesian RM anova and in post hoc comparisons I read BF10, U which means U?
could you help me?
U stands for "uncorrected", so it does not include the post-hoc correction term that comes from the prior model probability.
We'll clarify this in the table heading for the next release; I've made it an issue on our GitHub page.