agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games







Comments
Hi Toc,
I suspect that your analysis is not correct. But I'm having trouble understanding why you made the specific comparisons that you have. Could you explain the logic behind what you've done?
As it happens, I just posted a blog about interpreting Bayesian Repeated Measures output:
Cheers!
Sebastiaan
Check out SigmundAI.eu for our OpenSesame AI assistant!
At least (c) seems the other way around
E.J.
Hi Sebastiaan,
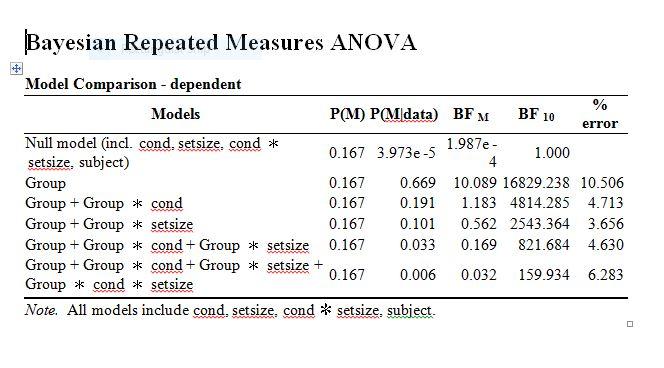
Thanks for your comment and sharing the link. I find it useful. Ok, here it goes. I have two separate studies. Study 1 has two factors: cond and setsize. Study 2 also has two factors: cond and set size. I have ran separate Bayesian repeated measures ANOVA for both studies and everything seems fine. Therefore, I want to compare the two studies to see if performance is better in study 1 compared to study 2 and if it is, whether the advantage is mediated by cond and set size. In fact, the analysis is analogous to Mixed-factorial ANOVA, where study 1 and 2 (designated as group in the output) is between subject factor and cond and setsize as within subject factors. As you can see from the output, there is overwhelming evidence for H0 for the effect of group, indicating differences in performance between the two studies. So I'm interested in knowing if:
a) there is interaction between group and cond. That is whether performance the effect of condition is higher in study 1 than study 2
b) there is interaction between group and setsize. That is whether performance the effect of setsize is greater in study 1 than study 2
c) whether there is a 3-way interaction: group x cond x setsize.
Following the analysis and applying the transitive formula, I compared:
a) the model containing group, cond, and setsize (5th row in the output) with the model containing group and setsize (3rd row) = 821.684/2543.364 = 0.32. Therefore, I concluded there is evidence against the interaction (i.e., Group x cond)
b) the model containing group, cond, and setsize (5th row in the output) with the model containing group and cond (2nd row) = 821.684/4814.285 = 0.172. Also, I concluded there is evidence against the interaction (i.e., Group x setsize)
c) for the 3-way interaction (i.e., group x cond x setize), I compared the model on row 6 with the model on row 5 = 821.684/159.934 = 5.13. Thus, I concluded there is evidence for the interaction as H0 is supported. However, as E.J. said, it should be the other way round, that will then be 159.934/821.684 = 0.19. In that case, it is fair to conclude there is evidence against the 3-way interaction.
I hope I have made this clearer now. My question then is, is the analysis and interpretation correct?
Thanks for your input,
Toc
Hi,
If I understand correctly, you have marked a whole bunch of model terms as 'Is Nuisance'. Since none of the terms are really a nuisance (?), I assume you did this to reduce the number of models in the table so that direct model comparison becomes feasible. Is that right?
I wouldn't do that. What I would do is unmark all your terms as nuisance. This will give you a big, messy model table. But you can then apply the Baws Factor logic from the post that I linked to above to arrive at the evidence for specific terms. Does that make sense? It takes a bit of manual labor, but it's not difficult.
Cheers,
Sebastiaan
Check out SigmundAI.eu for our OpenSesame AI assistant!
Thanks Sebastiaan. Yes, you are right. I added cond, set size and cond x setsize as nuisance variable to allow for direct model comparison. I have read your post on Baws Factor, though it takes time but its very easy and straight forward.
Once again, thanks for your support and all suggestions. Much appreciated.
Cheers,
Toc
Hi Sebastiaan, given that the Baws factor is derived from P(M|data), how would one go ahead and report the result since I noticed most people report Bayes factor? So for instance, in a paper where I'm reporting three separate experiments, Experiment 1 and 2 have two factors each. The interpretation was based on information from BF10 (transitive formula applied), hence in the write-up I mentioned for instance, there is a compelling evidence against the null model for the interaction between factor 1 and factor 2 (Bayes factor = 23.37 or BF10 = 23.37). Then I come to my third experiment where I used Baws factor, will I still be reporting Bayes factor or Baws factor? Obviously the reviewer might ask, why the sudden change in terminology. Also, how do I reference Baws factor in my paper?
Thank you once again for all your suggestions.
Cheers, Toc
Hi Toc,
I think Sebastiaan was not beging serious when he proposed "Baws" as a name. You might just want to describe what models you were averaging over to compute the inclusion probabilities. Oh boy, we do need that manual and some decent help files...
Cheers,
E.J.
Ok, thanks E.J. for your response. I'm sure the manual will save some lives when it is out .
.
Cheers,
Toc