RM ANCOVA - calculating the bayes factor
A reviewer is asking us to perform bayesian analyses to quantify strength of evidence for the null. I am new to Bayesian statistics, but luckily JASP is really straightforward! I do have some questions however. I performed a bayesian RM ANCOVA, with a within subjects factor (under the factor 'time', with 2 levels), a between subjects factor (group randomisation), and a covariate (RCQ).
My first question is, if you want to do the analyses to evaluate the strength of evidence for the null, what bayes factor do you select in the analyses; B10 or B01? For the analyses I did, I selected the B01 since I believe this gives results on how much better the data predicts the null hypothesis compared to the alternative hypothesis?
Then I wanted to calculate the bayes factor. I found an article (Bayes like a Baws: Interpreting Bayesian Repeated Measures in JASP, by Sebatiaan Mathôt) on how to calculate the Bayes (or Baws) factor when you have multiple interaction terms, but I am wondering if this is the correct way to calculate the factor.
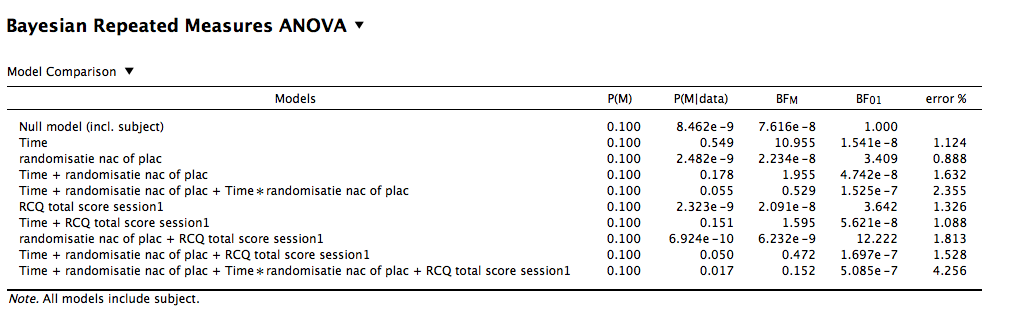
I've added the results table below. Based on the aforementioned article, I summed all P(M|data) of the models with the interaction term and divided that by the summed P(M|data) of the 'corresponding' models without the interaction term. So in the example below I performed the following calculation:
Baws factor ((0.055 + 0.017) / ( 0.178 + 0.050)) = 0.32
But is this the correct calculation, or do I need to do it differently?







Comments
Hi Mieke,
Nice to hear that you read my post :-) And yes, assuming that you're interested in the
Time * randomisatie nac of placeinteraction, the calculation is correct. So there is evidence against this interaction.Cheers,
Sebastiaan
Check out SigmundAI.eu for our OpenSesame AI assistant!
Hi Sebastiaan,
Thanks for the quick response! And for the very clear post of course!
I am indeed interested in the interaction. So how do I interpret this? Originally, I performed a parametric rm ancova, and there was no significant interaction (e.g. no treatment effect on the dependent variable). So the reviewer requested bayesian analyses to see if there is evidence for the null. So no evidence that there is an effect and no evidence that there is not an effect? I'm having trouble comprehending what this means. Could you help me with this?
Best,
Mieke
There is evidence for the null, the null being the absence of an interaction in this case. So that makes perfect sense given that the interaction was non-significant in the regular ANCOVA.
I think this may be the source of confusion:
That's correct, but it only affects the columns that contain a Bayes Factor. You directly took the P(M|data), and used that to calculate your own BF10. If you wanted to have a BF01 instead, it would be:
BawsFactor01 = ( 0.178 + 0.050) / (0.055 + 0.017) = 3.17
Does that make sense?
Check out SigmundAI.eu for our OpenSesame AI assistant!
Yes, that makes sense. I have one more question about the interpretation of the BawsFactor. In this case (BawsFactor01=3.17), can I state that there is sufficient evidence for the null hypothesis? Or otherwise, how do I report this result?
This is a table from Wetzels and colleagues with some rules of thumb. So I would describe it as 'substantial evidence against the existence of an interaction'. Something along those lines should be fine.
Check out SigmundAI.eu for our OpenSesame AI assistant!
Thank you so much for your help, I really appreciate it!!!
For an interpretation of the strength of evidence that a Bayes factor provides, see the cartoon here: https://osf.io/3acm7/