agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games


Comments
Hmm. Let me ask a team member and get back to you.
E.J.
OK, based on some quick research by Johnny van Doorn, it appears that the formula is in need of correction when there are within-subject factors. This is a good catch. We'll fix this in our upcoming release.
Cheers,
E.J.
Well, glad I could help !
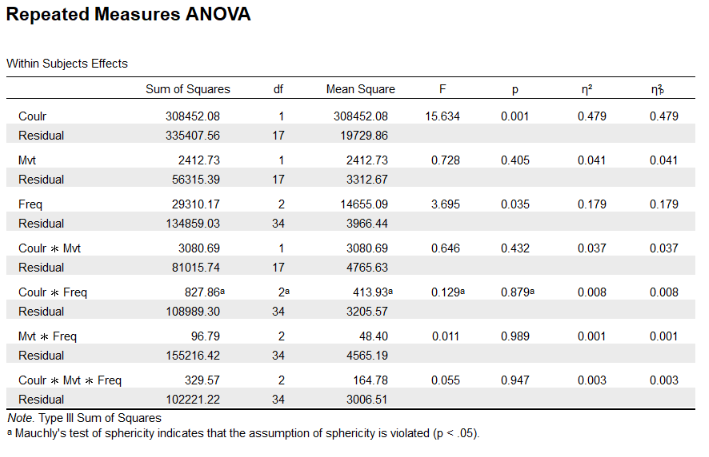
I've done my η² by hand and I believe partial η² are correct, the error seems to come from the η² computation (Levine & Hullett 02).
Can you guys keep this thread posted when this is fixed ?
cheers,
Raph
Yes, Johnny will look into it when he returns from a conference and we'll update you on our progress.
E.J.
Hi Raph,
Thank you for bringing this to our attention, and my apologies for the tardy reply. After reading up on effect sizes for within subjects designs, and consulting some of the true statistics guru's at our department, I have come to the conclusion that the eta squared as reported does not differ from the partial eta squared when dealing with a design with only within subjects factors. If you were to add a between subjects factor, the partial eta does differ from the nonpartial eta.
This has to do with the formula used to compute the two effect sizes. For the nonpartial eta squared, the sum of squares of the effect is divided by the total sum of squares, whereas the denominator for the partial eta squared is the error term of only the effect. If you were to have only one factor, this means that the partial eta squared and nonpartial eta squared does not differ, as the error term of the effect constitutes the total error term. This is also how it is described in the article you linked.
The tricky thing with within subjects factors is the way the total error term is calculated. JASP (and SPSS for that matter) gives separate total error terms for each within subjects factor. It is not possible to sum these error terms (for a "total total error term"), because that would result in errors being counted double (or triple if you have three-way design) as a result of the within subjects design and would therefore provide a distorted image of the fit.
If attached a little example from the Andy Field book to illustrate the way these total error terms are made up. Here we have two within subjects factors (Looks and Charisma, both with three levels) and one between subjects factor (Gender). In this example, the partial and nonpartial eta squared do differ from each other, as there is a between subjects factor. So the denominator for calculating the eta squared for Looks is 20779.6 + 3944.1 + 882.7 = 25606.4, or the total error term (looking only within the within subjects factor of Looks). For the partial eta squared, the sum of squares from the interaction is not counted anymore, so the denominator there is equal to 20779.6 + 882.7 = 21662.3, or the error term of the effect only. In both cases the numerator is equal to 20779.6, yielding the provided effect sizes. If I were to remove the factor Gender from the model, both of the denominators would be equal and yield the same result for eta squared and partial eta squared.
So in short, the similarity of the effect sizes in your case is due to having only within subjects factors, and because of the way the total sum of squares are calculated in that case (i.e., only total within the within subjects factors), the partial and nonpartial eta squared yield the same result.
I hope this clarifies your query. I do have to say it's a bit of a niche issue, and many textbooks I consulted shy away from discussing this topic, so if you have any more questions I'd be happy to help you sort those out!
Kind regards,
Johnny
Hi. I have a question about the eta squared when conducting a mixed design ANOVA. When conducting a mixed design ANOVA (2 within and 1 between factors) JASP and JAMOVI give me the same p values and the same partial eta squared. However, JAMOVI and JASP give me different eta squared. While JASP gives me a n² number very close to the np², JAMOVI gives a n² very different from the np². (e.g. np² = .138, JAMOVI gives me n²=.21 while JASP n²=.136).
I know that devs here are not responsible for the JAMOVI outputs. But I would like to ask if someone can tell me why these eta squared are so different.
Cheers.
Hi. I have a question about the eta squared when conducting a mixed design ANOVA. When conducting a mixed design ANOVA (2 within and 1 between factors) JASP and JAMOVI give me the same p values and the same partial eta squared. However, JAMOVI and JASP give me different eta squared. While JASP gives me a n² number very close to the np², JAMOVI gives a n² very different from the np². (e.g. np² = .138, JAMOVI gives me n²=.21 while JASP n²=.136).
I know that devs here are not responsible for the JAMOVI outputs. But I would like to ask if someone can tell me why these eta squared are so different.
Cheers.
Dear Gabriel,
Thanks for bringing this to our attention. We will look into it and keep you posted!
Cheers,
E.J.
Hi Gabriel,
We use the approach I outlined in my previous post - you can read more about it here.
I am not sure what JAMOVI uses - maybe you can contact them on their github page.
One thing that could cause a discrepancy is that different types of sum of squares were used to obtain your results - this leads to different values for the effect sizes. However you do say the p-values and partial effect sizes are the same so that is probably not the case.
Cheers
Johnny
Hi.
Thanks for the replies!
Cheers.