agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games







Comments
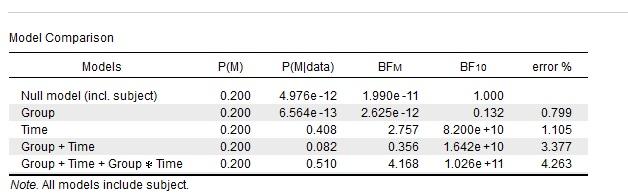
The model with the interaction is the best. To see by how much, it is easiest to select "compare to best model".
Cheers,
E.J.
Hi E.J.,
The model with the interaction is 1.25 better than a model with Time only. It's only better by a bit, but would you then conclude that there is support for an interaction? Or would you be more careful in stating this?
That level of evidence is almost completely nondiagnostic. If you have strong reasons to include the two main effects then you can focus on the two main effect model compared to the full model that also includes in the interaction (this is the same as defining the two main variables "as nuisance"). If the approach is more exploratory than you can explain the complete table.
I specifically expected an interaction between Group and Time, so to assess whether this is supported by the data I always need to compare it to the two main effects model (i.e., adding these as nuisance factors) and cannot compare it to a main effect model of Time. Is this correct?
What I was wondering; is it accepted to add Group and Time as nuisance factors and then state that there is no support for an interaction, and then follow that up with describing the complete table?
If you add group & time as nuisance, then you are comparing the full model to the two-main effects model. This yields BF=6.25 in favor of adding the interaction. So that's a little better than "no support"
Hm, I thought I had this figured out, but I started reading about the 'Baws factor' (which it seems is an arbitrary term), but is implemented in the latest version of JASP under the 'Output' and then 'Effects' boxes.
One of my reviewers argues that for the interaction I should actually use this part of JASP. I am not sure if I need to do this, if I want to show evidence for the interaction. And if so, should I then use 'across all models' or 'across matched models'?
I'd report report the entire model comparison table. Yes you can test the two main effects model against the model that also includes the interaction. It seems to me that this is the most intuitive analysis. Maybe the table will look more compelling if you select "compare to best model" and then "BF_01": you will see the best model on top, and then the BFs will indicate how much more support the best model receives compared to each of the others.
Cheers,
E.J.