agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games







Comments
Hi Alon,
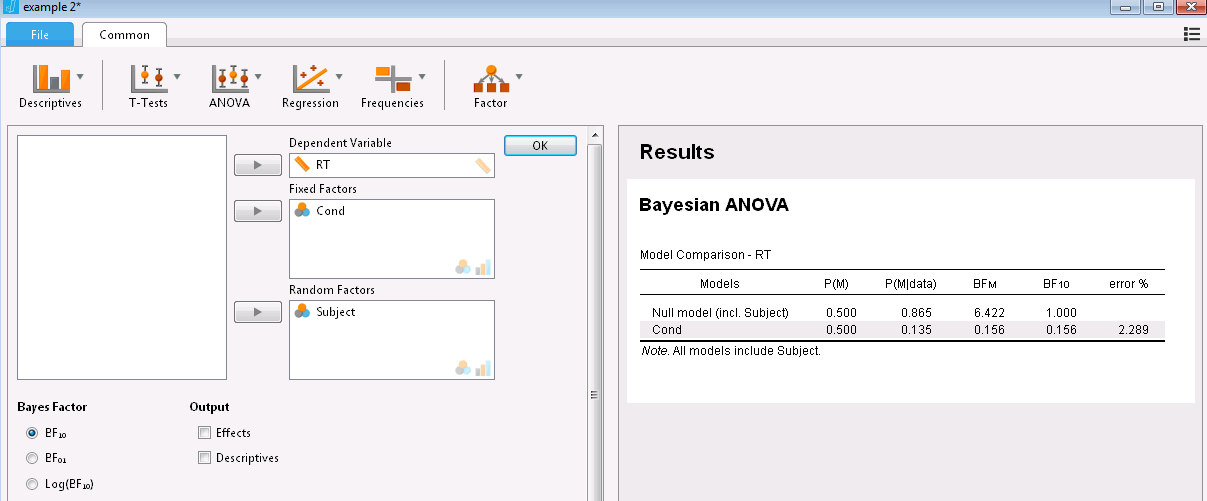
This is more the expertise of Richard Morey, so I'll attend him to this, as well as Quentin Gronau. For what it is worth, I think you are right. The Bayesian ANOVA in JASP is really a Bayesian linear mixed model. Perhaps there is a post on how BayesFactor deals with this...
Cheers,
E.J.
Hi Alon,
I agree with E.J.. The Bayesian ANOVA in JASP is implemented using the Bayesian linear mixed model framework from the BayesFactor package by Richard Morey. That is, the Bayesian repeated measures ANOVA in JASP is a Bayesian linear mixed model with random participant effects. Therefore, to me it seems reasonable to add subject as a random factor in your case. With respect to the fact that you have multiple observations for each participant in each condition: In the paper by Jeff Rouder and colleagues (https://doi.org/10.1016/j.jmp.2012.08.001) on which this Bayesian mixed model implementation is based it is mentioned in at least one sentence that multiple observations per condition can be handled within this framework:
"This term [the interaction between the random participant factor and the condition/stimulus factor] may be estimated if the design is replicated, that is, each participant yields several observations in each condition" (p. 367).
Furthermore, here are two links that provide additional information about mixed models in BayesFactor:
bayesfactorpcl.r-forge.r-project.org/#mixed
https://cran.r-project.org/web/packages/BayesFactor/vignettes/compare_lme4.html
Cheers,
Quentin
Thank you E.J. and Quentin