Bayesian Comparisons
Hello all,
I have some questions regarding JASP's Bayesian post-hoc test for ANOVA.
How are the priors / posteriors / BFs computed?
Using the tooth-growth sample data,
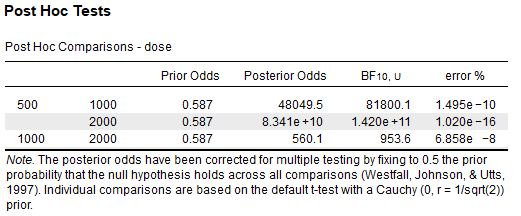
I have conducted the same t-tests in R using BayesFactor and found the BFs to be the same.
`> list("500 vs 1000" = df %$% ttestBF(len[dose=="500"], len[dose=="1000"]) %>% extractBF(F,T),
- "500 vs 2000" = df %$% ttestBF(len[dose=="500"], len[dose=="2000"]) %>% extractBF(F,T),
- "1000 vs 2000" = df %$% ttestBF(len[dose=="1000"], len[dose=="2000"]) %>% extractBF(F,T))
$'500 vs 1000'
[1] 81800.12
$'500 vs 2000'
[1] 142002125644
$'1000 vs 2000'
[1] 953.5515`
Does this mean that posterior odds are calculated as BF*(prior odds)? In that case, the correction for multiple comparisons is not on the BF itself, but on the posterior odds - wouldn't we want the correction on the BFs themselves?
Also, I've tried looking up Westfal, Johnson and Utts's paper, but I still don't understand how the prior odds are calculated.
Constrained / Restricted models vs. post-hoc tests
Richard has previously detailed in his (old) blog how to calculate BFs for specific hypotheses regarding restricted / constrained models.
When should one conduct these tests as apposed to the methods used in JASP for post-hoc tests?







Comments
Hi MSB,
Cheers,
E.J.
Hi E.J.,
3) If the (corrected prior odds) = (uncorrected prior odds)×correction.X, then applying (corrected BF) = (uncorrected BF)×correction.X would still result in the same posterior odds, which would still be equal to (uncorrected prior odds)×correction.X×(uncorrected BF).
I understand why applying the correction to the prior odds makes theoretical sense, but I think the adjustment would make practical sense on the BF since (as far as I can see) people mostly report BFs and not posterior odds.
5) Would the post-hoc method used in JASP work also for specific planned contrasts (for example by taking the t statistic from
lsmeans::contrastfunction and computing the apropriate BF usingBayesFactor::ttest.tstat)? Or do you think that in that case using model restrictions to be more suitable?Thanks,
M
Hi MSB,
The correction for multiplicity is usually always through the prior odds. This is even the case in parameter estimation, where you have to spread out your prior mass across more options (imagine a discrete parameter space with an increasing number of possible values). So it is sort of built-in from the start.
For contrasts, the model restrictions are more sensible. We will implement these in JASP too.
Cheers,
E.J.
But if you implement model restrictions into JASP then I will have learned R for nothing!
Thanks E.J.!
Hello.
I have understood why we have to correct the prior odds, but I want to know exactly how I calculate this prior odds. I have read Westfall, Johnson & Utts(1997), but I got some different values from shown here.(may be my mistake or I do not understand well...:(
Would you tell me other articles or blogs written in detail?
If you send me an Email I can forward you the internship report by a student, Tim de Jong, who worked on this.
E.J.
Dear E.J.
Thank you very much!!