Bayesian mixed ANOVA
Hi all, as a(n almost) complete beginner in Bayesian statistics, I have a probably very simple and stupid question!
I have conducted a study with a 2(between) x 5 (within) subjects design. Participants who were classified as either healthy or depressed and completed an object rotation task with 5 levels of angular disparity. The prediction was that the between factor would not affect the outcomes of the OR task in any way, which is why I conducted a Bayesian analysis. Now to make this case, I wanted to show that neither the main effect of the between factor, nor its interaction with the within factor affect the BFs over the null model. This would be my first question: are these two comparisons indeed what I need to make my case?
For the analysis I checked the main effect of the within factor as nuisance, so that I get the model comparisons between the (null + within) model for the two effects involving the between factor. This is what it looks like in JASP:
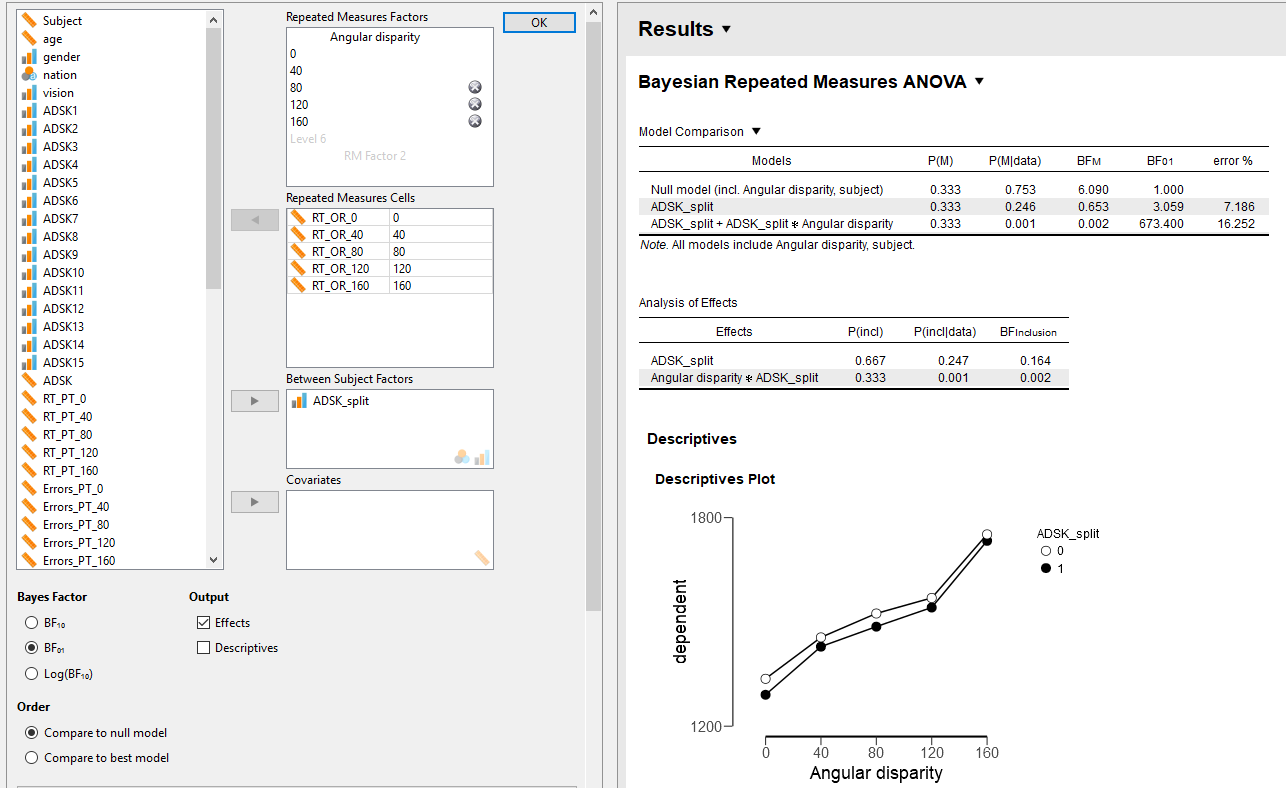
So the results I get are:
a) Individual BFs for the effects (~3 and 673 in favor of the null for the main effect and the main effect + interaction models, respectively).
b) The BFinclusion statistics. From what I could gather from this forum, these are the comparisons for the models including one specific effect with all other models in a 10 format (so I must reverse them to get to my 01 metric). So the BFinclusion for the two models with the main effect is basically ~6 and the one for the model with the interaction is 500. If I understood this correctly, the data are (6x/500x) more likely under the null+within modell than under the model that includes the additional effect(s). This is my second question: is this the correct interpretation?
My third question is which of these statistics do I report? I believe that the BFinclusion is the most important statistic. Or should I report both a) and b). What is the correct way of doing this?
Finally: How would I report these results? Do I just report the BFs or should I provide accompanying F-values from a frequentist ANOVA? How would you evaluate this paragraph of results:
“To evaluate the impact of the depression on object rotation performance, a 2 (Depression: depressed vs. non-depressed; between) x 5 (Angular Disparity: 0° vs. 40° vs. 80° vs. 120° vs. 160°; within-subjects) Bayesian mixed models ANOVA was conducted. Models involving the main effect of Depression and the model including the Depression x Angular Disparity interaction were both compared to models not involving these factors. As a result, Bayes Factors for the inclusion of these two effects were derived, which quantify the extent to which the data support the inclusion of the main effect or interaction effect of depression. These were BF01 = 6 for the main effect models and BF01 = 500 for the interaction model. Bayes factors of this magnitude are often conventionally described as moderate and overwhelming evidence against the inclusion of the main effect and the interaction, respectively. Thus, it seems more likely that depression did not affect object rotation performance.”
I would greatly appreciate your help!
Best wishes,
Thorsten.







Comments
Hi Thorsten,
Thanks for presenting the case so clearly. Yes, I think you are spot on. It is interesting that there is so much evidence against the interaction -- I bet this is because you have 5 levels of disparity. As an aside, this is valuable information for planning an experiment: the outcomes may be much more diagnostic if you include multiple levels within a factor.
Oh, yes, the paragraph is fine, but I would put an annotated .jasp file on the OSF, so that the complete output is easily and publicly accessible.
Cheers,
E.J.