agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games
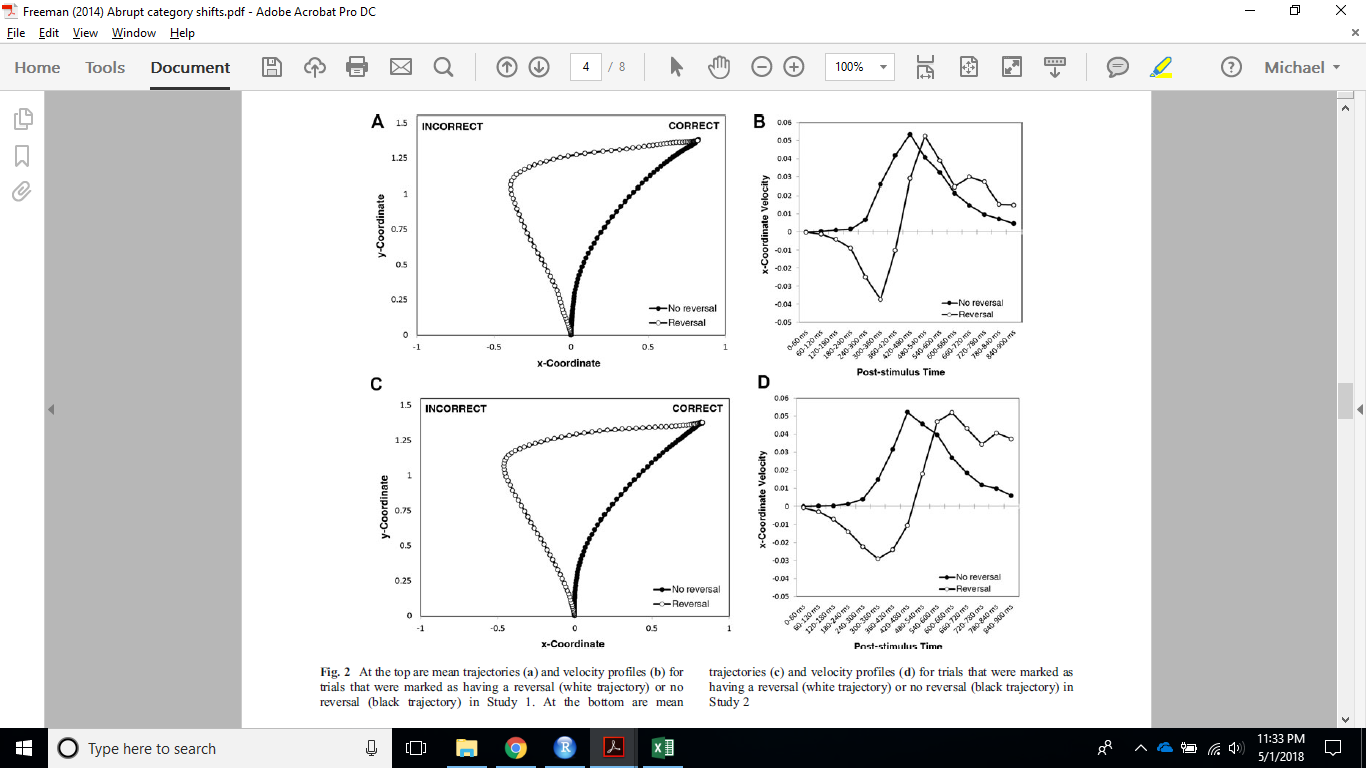








Comments
Hi Mike,
regarding one: yes, it is possible to do this in the mousetrap R package.
Here are two examples:
Example 1 that is close to the Freeman (2014) plots:
Example 2 based on time-normalized trajectories:
Best,
Pascal
Regarding two:
I don't think this assumption is correct. I think the MD threshold of 0.9 is applied on the raw MD values calculated by MouseTracker. As MouseTracker transforms the original pixel values into its own metric (x values between -1 and 1, y values between 0 and 1.5) the resulting MD values (and accordingly the threshold) are also in this metric.
Together with Barnabas Szaszi and a few colleagues from Budapest we recently generalized the MD threshold technique to be able to identify multiple changes of mind (one paper that uses this method can be found here). I have also implemented this in the mousetrap R package including a function that translates Freeman's threshold into a value that fits for the specific layout and metric of any new study. The code is not yet included in the package but I will make it available in the next weeks - just let me know if you are interested earlier.
Hi Pascal,
Thank you for the helpful response! I have a couple of follow-up questions.
Regarding velocity (1):
I noticed that you did not include the remapping code.
MT <- mt_remap_symmetric(MT)Should remapping be skipped for velocity? Or did you assume that remapping would have been done earlier?
Regarding velocity (2):
I'm running a memory recollection study where participants are allowed up to 8 seconds to try and recall their response. As you can imagine, the histogram of the response time for this task has a verrrrrrrrrrrrry long tail/skew with the number of trials dropping off precipitously after about 3 seconds or so. Given this, I feel like I should use time-normalized trajectories to look at velocity. I know you prefer to look at absolute time but given my very wide range of response times, I think I should use time-normalized trajectories for velocity. Does this seem reasonable? There is also a secondary concern that the interval size for averaged trajectories seems somewhat arbitrary. For example, I'm not quite sure why Freeman (2014) used a size of 60 ms.
Regarding your plotting code:
I noticed that you did not include the subject_id = "subject_nr" argument in the code. When should that argument be specified and when should it not be? Don't we always want to aggregate within a participant before aggregating within a condition?
Regarding your MD code:
Thank you for that paper. It looks extremely helpful. And thank you correcting my false assumption. I do not need the code immediately and can easily wait until the package is updated. I have signed up to the mailing list and will keep my eyes out for an email on it.
Infinite thanks and appreciation for your help!
Hi Mike,
Regarding velocity (1): yes, it definitely is best to remap the trajectories beforehand (the example trajectories in mt_example are already remapped).
Regarding velocity (2): that's a good point and unfortunately (in my view) there is no really good solution in cases where the response times differ substantially across trials. In principle I agree with you that it makes sense to use the time-normalized trajectories. However, this does not completely solve the problem if you compare trajectories of different length since the temporal resolution would then be quite different between trials. You could think about using time-normalized trajectories but doing separate analyses for trials of different length (e.g. below and above 4 s).
Regarding the aggregation procedure: good point. I think that in general it makes sense to first aggregate within and then across participants. However, if the trial number differs substantially between participants (which might e.g. happen in the example above if you split your analyses for different subsets of trials) this might lead to strange results so in this case it is probably best to leave it out.
Hope this helps! I think that you are raising important questions and in many cases I can only provide a suggestion and no definite recommendation.
Best,
Pascal
Thank you for all your assistance!
Hi Pascal,
I just read your paper using AOI (Szaszi, Palfi, Szollosi, Kieslich, & Aczel, 2018) that you cited earlier in this discussion. I really liked the techniques used therein and think they'll be quite valuable.
In your post above, you mentioned that you were going to include Freeman's version of MD used to discriminate between smooth and abrupt trajectories and areas of interest (AOIs) in the R mousetrap package. I was just following up to see if those are publicly available yet. I have a few research questions that would benefit by using those measures.
Thanks again for continued help and assistance! Also, happy to see MT has finally been given it's own forum!
Hi Mike,
sorry for the delayed reply - I was on holiday and afterwards gave a workshop at a summer school (on mouse-tracking ).
).
The MD and AOI classification functions are not included in the mousetrap package yet, as they still require a lot of testing and documentation. However, I am happy to email the current development version to you if you send me your email address.
Best,
Pascal
Hello, Sorry for the trouble but I have another velocity question.
Sometimes when I create velocity plots, they have broken segments within them. For example, when I create this plot using averaged bin sizes of 30ms, I get the following discontinuous graph. How is it possible for velocity to be missing in the middle of the curves?
Here is the corresponding code:
MT_EXP2 <- mt_import_mousetrap(d.EXP2, timestamps_label= "timestamps_get_MT", xpos_label = "xpos_get_MT", ypos_label = "ypos_get_MT") MT_EXP2 <- mt_remap_symmetric(MT_EXP2) MT_EXP2 <- mt_align_start(MT_EXP2) MT_EXP2 <- mt_derivatives(MT_EXP2, dimensions = "xpos", absolute = FALSE) MT_EXP2 <- mt_average(MT_EXP2, interval_size = 30, max_interval = 900) MT_EXP2_DS <- mt_subset(MT_EXP2, CUESIDE=="DS") mt_plot_aggregate(MT_EXP2_DS, use = "av_trajectories", x = "timestamps", y = "vel", color = "CUE") + geom_line(size=2) + scale_color_manual(values=c("red", "black")) + ggtitle("EXP 2 - SHORT DUR (60ms bin)") + theme(plot.title = element_text(hjust = 0.5)) + scale_x_continuous(breaks = seq(30, 9000, by = 30))But when I change the interval size to 60 ms, the curve is continuous.
Clearly, the bin size is the crucial factor. I just don't understand why velocity would be missing for the middle of a trajectory?
Thank you for any guidance you may be able to provide on this!
Hi Mike,
that's weird indeed! Without the raw data to reproduce it I have to admit that I don't know the answer.
Could you try to replace
y="vel"withy="xpos"to see whether there is a general problem or whether this problem is specific to the velocity?Best
Pascal (note: I am currently traveling for the next two weeks without steady internet access, so my replies might be a bit delayed)
Hi Pascal,
If it helps, I can provide the data. What method would be easiest?
I replaced y = "vel" with y = "xpos" and got a similar problem (pictured below). My code followed the same work flow as above.
Thank you for your continued help with this!
Hi Mike,
if the problem happens also with the xpos, my guess would be that the cause is the following:
there could be a few (probably very few) trials in the mismatch condition where the time passed between two adjacent logged positions is > 30ms which causes missings for specific intervals if the interval size is too small. But this is just a guess so you would have so check it in the raw data.
If this is the cause, then the solution would either be to exclude the trials with the missing, to increase the interval size or to use mt_resample to add the missing positions. However, the latter solution could bias the velocity calculation so probably it is easiest to use a larger interval size or exclude the trials.
Best,
Pascal
Hi Pascal,
Thank you again for your help and apologies for the delay in my response. The only issue I see with increasing the bin size is that it may unintentionally obscure differences in velocity peaks. For example, when using a bin size of 30ms, the solid black line appears to peak slightly before the solid red line (see purple circles). [Whether or not this is statistically meaningful is a different story.] This is shown below.
However, when I use a bin size of 60ms, the velocity peaks appear to occur at the same time. But this appears to be an artifact of the bin size obscuring small differences. Unfortunately, these small differences in the timing of the velocity peak--i.e., which peak occurs first--are theoretically relevant.
Thus, for theoretical reasons, I would prefer to use the smallest bin size possible, however resampling might not be a viable option if it biases the data. I'm not entirely certain I know how I would identify trials where the mouse stops moving for a duration greater than the bin size. Is this done using the hover_threshold in the mt_measures function?
Just as a general note, resampling it did seem to work. So your diagnosis of the problem seems correct. I'm not sure how much the trajectories are biased, but it now looks as expected.
MT_EXP1 <- mt_import_mousetrap(d.EXP1, timestamps_label= "timestamps_get_MT", xpos_label = "xpos_get_MT", ypos_label = "ypos_get_MT") MT_EXP1 <- mt_remap_symmetric(MT_EXP1) MT_EXP1 <- mt_align_start(MT_EXP1) MT_EXP1 <- mt_resample(MT_EXP1, save_as="rs_trajectories", step_size=10) MT_EXP1 <- mt_derivatives(MT_EXP1, use = "rs_trajectories", dimensions = "xpos", absolute = FALSE) # calculate signed velocity based on movements along x dimension MT_EXP1 <- mt_average(MT_EXP1, use = "rs_trajectories", interval_size = 30, max_interval = 900) #60 ms AVGed bins;900 = max time, is a multiple of 60 # plot mean velocity across time per condition mt_plot_aggregate(MT_EXP1, use = "av_trajectories", x = "timestamps", y = "vel", color = "CUE", linetype = "CUESIDE") + geom_line(size=2) + scale_color_manual(values=c("red", "black")) + ggtitle("EXP 1 - LONG DUR (30ms bin") + theme(plot.title = element_text(hjust = 0.5)) + scale_x_continuous(breaks = seq(60, 9000, by = 30))Hi Mike,
glad to hear that resampling solved the problem.
I again thought about the potential biasing problem: I actually think that resampling itself should not bias the velocity calculation. The only bias that could occur is if a change in position simply was not recorded in the raw data due to the tracking being to slow. However, I think this is very unlikely to happen in practice as the standard sampling interval of 10 ms is usually short enough to capture the vast majority of position changes and this predefined sampling rate is usually met in most cases. You can use the mt_check_resolution function to determine how often it was met in your dataset (note that if it is not met the sampling interval is in most cases < 10 ms due to a click leading to an immediate recording - which is no problem - and larger intervals occur only very rarely).
One comment to your reply "I'm not entirely certain I know how I would identify trials where the mouse stops moving for a duration greater than the bin size.": I don't think that not moving the mouse would cause a missing recording of a position - this should be unrelated to the question whether the mouse was moved or not moved - and in general should happen very rarely (see my point before).
One additional note: if you want to test for differences in peak velocity you can look at the vel_max_time variable that is calculated by mt_measures for each trial.
Best,
Pascal
Hi Pascal,
Thank you again for your thoughts. I've considered using the vel_max_time but I wasn't sure of two things. One, is the velocity absolute velocity? I have two distinct peaks and it is the second velocity peak that interests me (which is negative). I have looked at the documentation but it did not specify whether it was absolute or not.
Two, related to the first note, I am specifically interested in the second velocity peak. So if the first peak was higher than the second, that would confound the measure produced. That's why I didn't originally look at vel_max_time.
Thank you again for all your help.
Hi Mike,
mt_measures computes four velocity related measures:
vel_max: Maximum velocity (i.e. if there are both positive and negative velocities, the largest positive value)
vel_max_time: Time at which maximum velocity occurred first
vel_min: Minimum velocity (i.e. if there are both positive and negative velocities, the "largest" negative value)
vel_min_time: Time at which minimum velocity occurred first
If you have absolute or signed velocity values depends on the settings you use when computing the velocities in the mt_derivatives function (see documentation here).
If you have two positive peaks, mt_measures would only return the value and timestamp of the largest peak.
Best,
Pascal
Hi Pascal,
I've decided to use mousetrap's pregenerated velocity measures but I'm having trouble understanding how the measures relate to my plots. My velocity plot looks like this...
And when I create a summary line graph of the velocity_max_time measure, it looks like this:
Eye-balling the top graph, it looks like Match-DS (the solid red line) has a positive peak around 210 ms. But looking at the summary plot in the line graph, Match-DS appears to peak around 280 ms. I'm trying to understand why there is such a large discrepancy between the top plot and the bottom. Shouldn't they reflect the same thing?
Thank you for your help!
Hi Mike,
that's a good question. I think that there could be different reasons for this apparent discrepancy:
1) I just wanted to point out that the heading on your first graph says LONG DUR and the heading on your second graph says SHORT DUR so I just wanted to be sure that the same trials are the base for the two figures (and not trials with long duration in the first graph and with short duration in the second graph)?
2) As I don't know the underlying raw data: for the first graph, it could be the case that not all trials have data across the complete trial so it might be that not all trials contribute data to all time periods, whereas all trials contribute data to the second graph.
3) Even if the trial base is the same, there can be a discrepancy between the two graphs as they plot different things. In the first graph, the velocity "peak" around 210 ms might be caused by some trials with extremely high velocities in this period. Other trials with lower maximum velocities might have their peak at a different point in time but given their overall smaller peak velocities might not show up as a peak in the first graph. In the second graph all trials contribute equally regardless of the size of their maximum velocities.
Hope this helps!
Best,
Pascal
Hi Pascal,
1) Oops. I double checked the code. The plots are correct and from the same data set, even though one has the incorrect title.
2) Interesting. I wonder what could contribute to certain trials not having data across the entire trial. I understand how this could happen towards the end of trials, but 300 ms seems too short a time period for people to be successfully finishing their mouse click. I suppose resampling is not something that would fix that issue, is it?
3) Ah, so it could be that outliers are essentially skewing the data in the top graph but not the bottom.
4) This leads me to wonder if the velocity graphs can ever be trusted over the summary data. The top graph suggests that the solid black lines peak (both positive and negative) before the solid red lines. Yet, the summary data suggests the exact opposite.
Thank you again for your helpful comments!
Hi Mike,
regarding 2): you are correct in that this can only happen towards the end of the trial, i.e., if the response is given before the time interval that is depicted in the figure. So this explanation is probably not relevant if we look at early movements in the trial (as is the case here).
regarding 3): I would not necessarily call this outliers. We are simply looking at different types of information (time of maximum velocity regardless of its size in the second figure vs. time of the maximum of the mean velocities across the trials in the first figure). But in a way the explanation is correct as if all trials had similar velocity developments (in terms of their absolute sizes) both figures would likely lead to more similar conclusions.
regarding 4): I would agree with you in that if you are concerned with the time point of the peak velocities I would trust an analysis more that is based on the time points of the individual maximum velocities in each trial than an inspection of the aggregate velocity figure.
Best,
Pascal
Hi Pascal,
Quick clarification regarding vel_max_time and vel_min_time measures. I checked the documentation to try to figure this out on my own but I wanted to be certain since I didn’t exactly find what I was looking for.
I’ve remapped trajectories to the left side and set mt_derivatives(absolute = “False”). Then I produced vel_max_time and vel_min_time. My understanding is that vel_max_time corresponds to movement to the right-hand side of the screen (in this case, the unchosen option since everything was mapped to the left). Likewise, vel_min_time would correspond to time of greatest acceleration to the left-hand side of the screen (towards the chosen respond).
So using the solid red line from the picture below as an example.
vel_max_time = movement towards unchosen response on the right side (the peak above zero); i.e., commitment towards distractor
vel_min_time = movement towards chosen response on the left side (the peak below zero); i.e., commitment towards final response
Is this understanding correct?
HI Mike,
in principle everything you described is correct!
Minor points:
But, again, I'd say that on the technical level everything is correct.
Best,
Pascal
Excellent. Thank you!