Fluctuating Bayes Factors when recalculating based on same data
Hi,
I've noticed that the Bayes Factors for Bayesian Repeated Measures can fluctuate quite a bit when running the same analysis again on the same data. If my understanding is correct, some fluctuations are to be expected, because the analysis is not deterministic. However, the fluctuations are sometimes substantial.
For example, for the attached data file, the BF inclusion for target-match × distractor-match varies from 1.3 to 2.5. And I'm fairly sure that once the BF was actually above 3.0, which is what prompted me to look into it in more detail. (@Cherie reanalyzed this data based on a reviewer comment, and now suddenly there was evidence for this interaction where previously there was none!)
So how should we best deal with this? I realize of course that we're talking about relatively small fluctuations, and that zero evidence never becomes very strong evidence. But still, the fluctuations are sufficiently large to affect the interpretation.
For future releases, would it be possible to reduce the fluctuations by increasing the number of repetitions that JASP uses to estimate the Bayes Factors? (I assume that something like that happens behind the scenes.)
Cheers!
Sebastiaan
Sebastiaan
PS. Two example results for the same data:








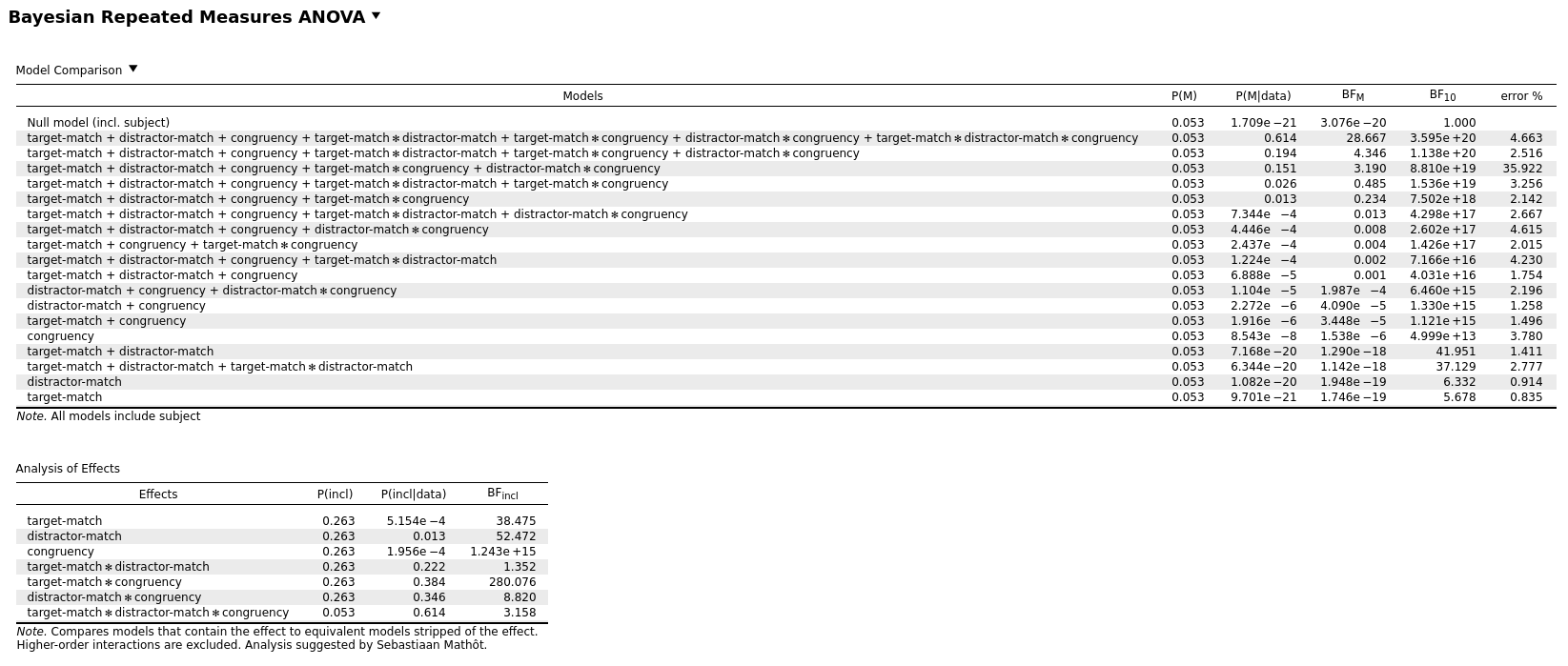


Comments
As you mention these fluctuations are minor (I would say that a change less than an order of magnitude is not substantial for a BF that is a ratio, after all).
What to do? Tread lightly - I think it is reasonable to explain in ms that due to instability in the calculation of this BF, you reserve judgment on it (I've actually seen something similar done in a paper, though the authors there did not use
Bayesfactor, butbrms+bridgesampling).Also, the %error will give an indication of the variability; if more stable results are desired, you can up the number of samples for the numerical routine under "Advanced options" -- this should bring down the error% (at the cost of taking longer). It would definitely be interesting to see whether the results can be improved upon, but it's a separate research project really.
Cheers,
E.J.
> I would say that a change less than an order of magnitude is not substantial for a BF that is a ratio, after all
From a statistical perspective, that's probably true. But imagine that you're reading a paper that reports a BF of 2, and compare that to the same paper that reports a BF of 8? Even as a statistician (but still human), would your interpretation be unaffected? Regardless of whether this is rational or not, people are definitely sensitive to these differences, so it's not ideal if these random fluctuations exist.
> if more stable results are desired, you can up the number of samples for the numerical routine under "Advanced options" -- this should bring down the error% (at the cost of taking longer).
After setting the Numerical Accuracy to 100,000 (so a 10× increase, I think), the analysis takes a bit longer (but not prohibitively so, perhaps a minute). The BFs still fluctuate, but they seem to do so a bit less.
Check out SigmundAI.eu for our OpenSesame AI assistant!
> but still human
I resent your assumptions, sir!
But yes, you are right - it would affected my interpretation somewhat 😞 (But that is a change of X4, what you described was a change of <X2, no?)
But maybe replace order of magnitude on base 10, with order of magnitude on base-e (which is basically the classical cut-offs for BFs)..