Conceptual question of interpretation of Bayesian rmAnalysis
Dear forum,
we are analyzing our data of EXPOSURE (n = 23) vs. SHAM (n = 15); pre-post, and we are assuming that there is NO interaction effect concerning our outcomes (here as one example: somatization).
____
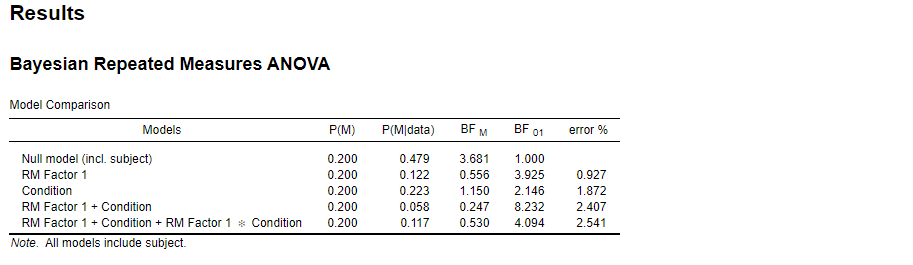
So we are interested in BF01 for the interaction (we don't really care about the main effects). So far, so good. Now, the results look as follows (see image). Is there any way to determine the absolute (not relative) evidence of the interaction?
____
I know from reading through a few papers that you are supposed to divide BF01 (main effects + interaction) by BF01 (main effects). But what you get out of there is the RELATIVE evidence including the interaction (whether it contributes any meaningful evidence to H0 relative to the main effects only model), right?
____
Just to further explain my problem: If BF01(main effects) was, let's say, 10. So this suggests that H0 is ten times likely than H1 for the main effect model. So we could imagine two groups that don't really change or differ at any point in time (hence we got a high BF01 for these main effects). Here, there is also no apparent interaction. Hence, the BF01 (main + interactions) could be even higher, as the null applies even more for this model; let's say, 20.
So, if BF01 (main + interaction) = 20 and BF01 (main) = 10; then 20/10 = 2, meaning that the evidence for H0 is even 2x stronger for the model including the interaction compared to the main effect model, correct?
In our data, it thus appears that entering the interaction does not further support the H0 (4.094/8.232 = 0.497), relative to the main effects model. Hence, adding the interaction does not really change the fact that there is overall support for H0 (main effects), but relative to a main effects model, entering the interaction does not provide any additional support for H0. I find the latter notion really confusing; does that mean we might be wrong in assuming that there is no interaction effect??? Is there any way to test evidence for/ against the interaction in absolute terms?
I hope you can help me in clarifying this.
Kind regards
Leonie







Comments
Hi Leonie,
This is a good example of why it is not universally true that an interaction is tested by comparing the main effects model to the full model. The entire pattern of results across all models is important. I would present the entire table and explain that the full model (including the interaction) is outpredicted by the null model. In fact, the null model is the best model in the set, so the comparison between two models that are outpredicted by a third may be of limited value.
Cheers,
E.J.