Default priors for Bayesian model comparison: Are they "ready-to-use" without further user input?
Dear all,
First off, thanks for your hard work! I really appreciate it.
after extensive searching I did not find a conclusive answer to my question, so here we go:
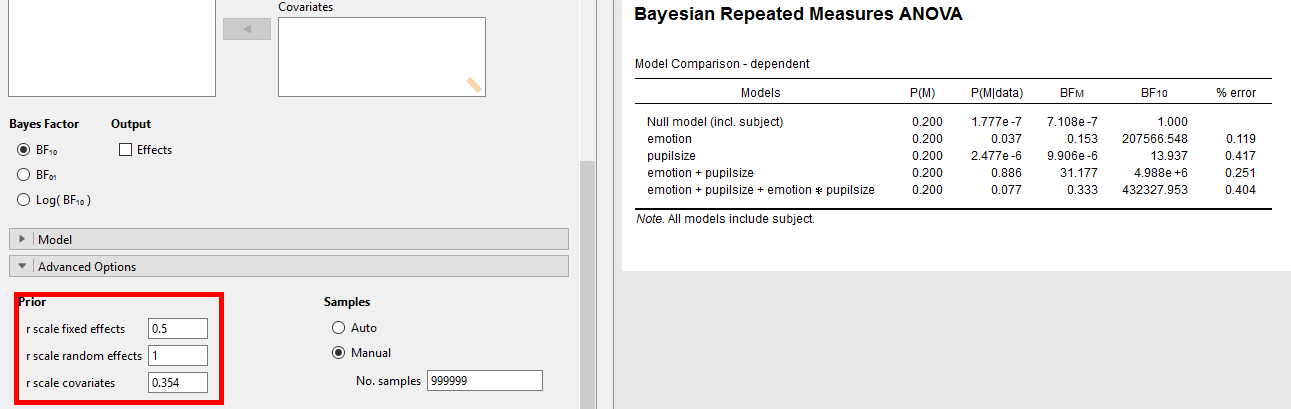
I am using the Bayesian Repeated-Measures in JASP 0.800 to test whether a model with or without an interaction is more likely given the data that I have. I am very happy with the results and would like to report them. However, I don't know what I should report with respect to the prior values being used.
It is important to mention that I don't want to make an informed guess about which hypothesis I myself deem more probable or about the effect sizes which I expect. Instead, I want the test to be as conservative as possible, explicitly assigning 50 % likelihood to both outcomes. My guess is that this is exactly what the default values in JASP are doing? I could not find a confirmation of this.
Jarosz & Wiley (2014) write "One issue that is often raised about Bayesian analyses is that they require a “prior”; that is, a prior probability distribution for the model parameters. Coming up with such an estimate can be problematic as it can require a certain amount of subjectivity and/or prior knowledge about the effect that is to be studied. However, a number of fairly objective priors have been developed, that make relatively few assumptions about the parameters."
TL;DR: When it comes to Bayesian Repeated-Measures ANOVAs, are the default values in JASP "fairly objective priors" that are ready-to-use? If not, how do I figure out which priors are appropriate?
I appreciate your comments!
Best wishes,
Thomas







Comments
The ANOVA conceptualized as a hierarchical linear mixed model where levels are clustered within factors following the approach of Rouder, Morey, Verhagen, Swagman, and Wagenmakers (2016). Here, the effects are shrinkage estimators (Efron & Morris, 1977) expressed in the effect size d where each factor gets a shared prior for its levels. The dispersion of these priors g is estimated from the data by a scaled inverse chi-squared-distribution with a single degree of freedom. The larger you set r, the greater is the dispersion, i. e. large effects become (a priori) more likely while small effects lose. if you lower r (if you expect a small group difference), small effects get more mass, while larger ones lose.
Yes, the default settings are meant to serve as an "objective" specification that can be used across a wide range of different scenarios.
Cheers,
E.J.
Thanks a lot for the fast responses!
Best wishes,
Thomas