Bayesian rmANOVA
Hi everyone,
for the analysis of one particular dataset, I have noticed a difference between the “regular” repeated measures ANOVA and the Bayesian rmANOVA.
There are two within-subjects factors "Segment" and "Context". Sample size N = 8.
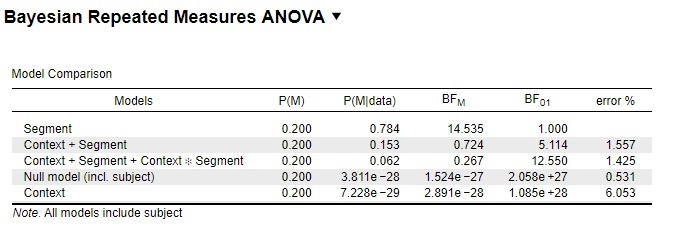
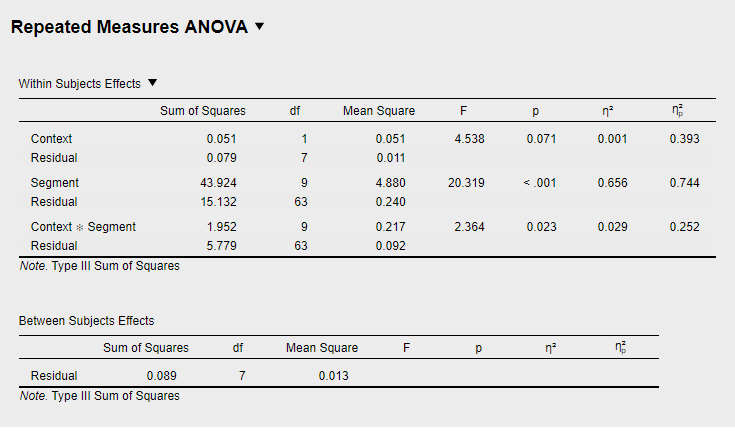
Whereas in the Bayesian rmANOVA, the model with the main factor Segment appears to be the most likely model, the “regular” rmANOVA yields a significant interaction between Segment and Context.
I have send an Email addressing this to E.J, his response is pasted down below as a starting point of further discussions:
"This is a good question for the JASP forum. I believe that two issues may play a role here:
1. Higher-order interactions can take all sorts of shapes. If these are not constrained by means of some sort of contrast analysis, the interaction is a highly flexible addition to a model, allowing it to account for all sorts of patterns; consequently, it will be penalized heavily.
2. JASP respects the principle of marginality, and this means that the interaction is not judged in isolation, but compared to the model with both main effects already present.
This is my best guess for now."
Any help in understanding the cause for the observed differences is appreciated.
Best regards,
Alexander


Comments
Hello Alexander!
Welcome to the JASP Forum. I am wondering if the observed differences involve the effect sizes? The significant frequentist interaction term has a quite small effect size while Segment's effect size is larger.
This is just a speculation.
Best
Anna
Hi Anna,
Thank you for your speculation, it is very welcome ;-).
I was thinking about something very similar when I read about the relation between effect size and bayes factors and that it is also dependent on the sample size.
For small sample sizes like the one in my study, it appears that effect sizes have to be rather large to result in a bayes factor that suggests evidence in favor of the H1.