Interpretation and reporting results of a Bayesian repeated measures ANOVA
Hello,
I am working through my first Bayesian repeated measures ANOVA and am would like to ensure that I 1) have done it correctly, 2) am interpreting the results accurately, and 3) understand how to write up the results clearly.
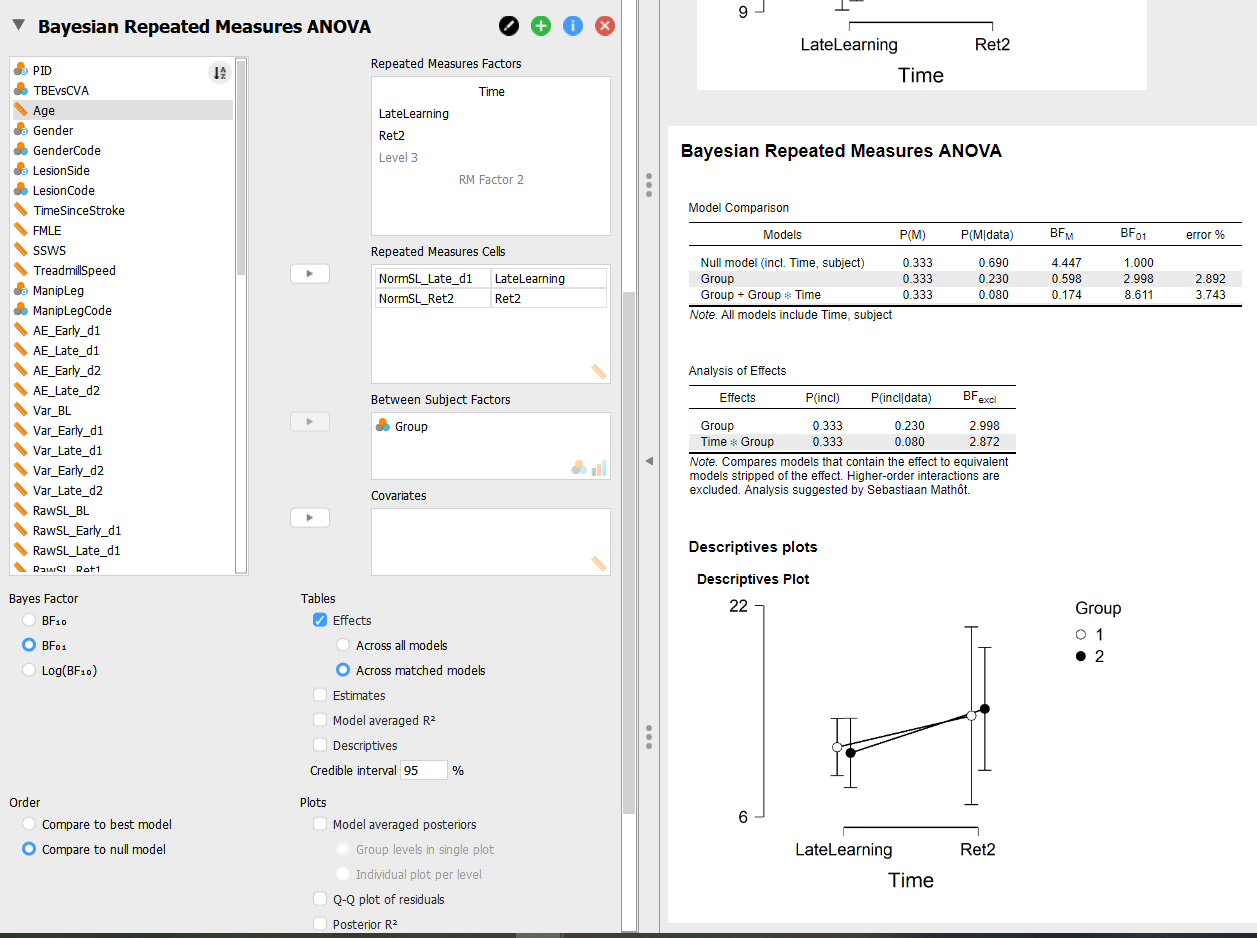
I am doing a 2 x 2 repeated measures, where I have measurements from 2 groups at 2 time points. I am most interested in the effect of group and a potential interaction. As a result, I have added Time to the null model...which brings me to my first question, is this is valid? In a frequentist ANOVA, you would report the main effect of time, regardless of your primary question; however, by adding Time to the null model I can not speak to the effect of time with this analysis. Per my research question, I am fine with this, but is this common practice with this type of analysis?
Based on the model comparison table (see image attached), I would conclude that the null model is 3 and 8.6 times more likely than a model including the main effect of group and a model with the main effect of group and the interaction of group and time. Is this the correct interpretation?
The analysis of effects table is where I am most hung up. I understand that there are 2 options for how to analyze this: comparing across matched models vs across all models. Based on my reading, the most conservative/accurate approach would be to compare across matched models rather than across all models to ensure that you do not attributing evidence to the interaction that is really due to the main effect. Is this correct and are there situations where you would want to compare across all models?
Based on the BFexlc from comparing across matched models, I would conclude that my data is 3 times more likely in models that do not include group than in models that do include group. Similarly, the observed data is 2.8 times more likely in models that don't include the interaction than those that do. Is this the correct interpretation?
Lastly, what should be reported in manuscripts: the BF for the tested models, BF excl, or both? Many manuscripts I have found are either not clear on what they have presented or only report BFincl/BFexcl. It seems that presenting both would be most comprehensive; however, the BFexcl seems to be more informative, so what is best practice?
Thanks!
MF


Comments
Hello,
I'm agree with your BF01 and BFexcl interpretation. I mean your analysis is consistent with guideline in this article : Bergh, D. Van Den, Doorn, J. Van, Marsman, M., Draws, T., van Kesteren, E.-J., Derks, K., … Wagenmakers, E. J. (2019). A Tutorial on Conducting and Interpreting a Bayesian ANOVA in JASP. 1–22. https://doi.org/https://doi.org/10.31234/osf.io/spreb
Concerning report you could look this : van Doorn, J., van den Bergh, D., Boehm, U., Dablander, F., Derks, K., Draws, T., Evans, N. J., Gronau, Q. F., Hinne, M., Kucharsky, S., Ly, A., Marsman, M., Matzke, D., Komarlu Narendra Gupta, A. R., Sarafoglou, A., Stefan, A., Voelkel, J. G., & Wagenmakers, E.-J. (2019). The JASP guidelines for conducting and reporting a Bayesian analysis. Manuscript submitted for publication. Preprint available at https://psyarxiv.com/yqxfr.
I'm discovering bayesian analysis too, so I hope this answer help you..
Have a nice day
KB
Hi MF,
Below are some answers to your questions:
"I am doing a 2 x 2 repeated measures, where I have measurements from 2 groups at 2 time points. I am most interested in the effect of group and a potential interaction. As a result, I have added Time to the null model...which brings me to my first question, is this is valid? In a frequentist ANOVA, you would report the main effect of time, regardless of your primary question; however, by adding Time to the null model I can not speak to the effect of time with this analysis. Per my research question, I am fine with this, but is this common practice with this type of analysis?"
In frequentist ANOVA this is not often done, but it is standard practice in frequentist hierarchical regression. And I'm fine with it.
"Based on the model comparison table (see image attached), I would conclude that the null model is 3 and 8.6 times more likely than a model including the main effect of group and a model with the main effect of group and the interaction of group and time. Is this the correct interpretation?"
Almost -- the BF is the evidence (relative predictive performance), so its the data that are more likely under the null, not the null that is more likely. That would be a posterior model probability interpretation.
"The analysis of effects table is where I am most hung up. I understand that there are 2 options for how to analyze this: comparing across matched models vs across all models. Based on my reading, the most conservative/accurate approach would be to compare across matched models rather than across all models to ensure that you do not attributing evidence to the interaction that is really due to the main effect. Is this correct and are there situations where you would want to compare across all models?"
There is an extensive discussion on this topic on this forum. I believe that in Don's ANOVA tutorial, referenced above, we also discuss the difference. With so few models in play, I'd be tempted just to present the results from the main table, and leave the analysis of effects for what it is.
"Based on the BFexlc from comparing across matched models, I would conclude that my data is 3 times more likely in models that do not include group than in models that do include group. Similarly, the observed data is 2.8 times more likely in models that don't include the interaction than those that do. Is this the correct interpretation?"
Yes.
"Lastly, what should be reported in manuscripts: the BF for the tested models, BF excl, or both? Many manuscripts I have found are either not clear on what they have presented or only report BFincl/BFexcl. It seems that presenting both would be most comprehensive; however, the BFexcl seems to be more informative, so what is best practice?"
I generally favor complete reporting (so both). This can always be done in an (annotated) JASP file online (e.g., on the OSF), or any online appendix. What is most informative depends on the context. The more models are involved, the more interesting the analysis of effects becomes.
Cheers,
E.J.