Very discrepant results from Repeated-Measures ANOVA and Bayesian R-M ANOVA

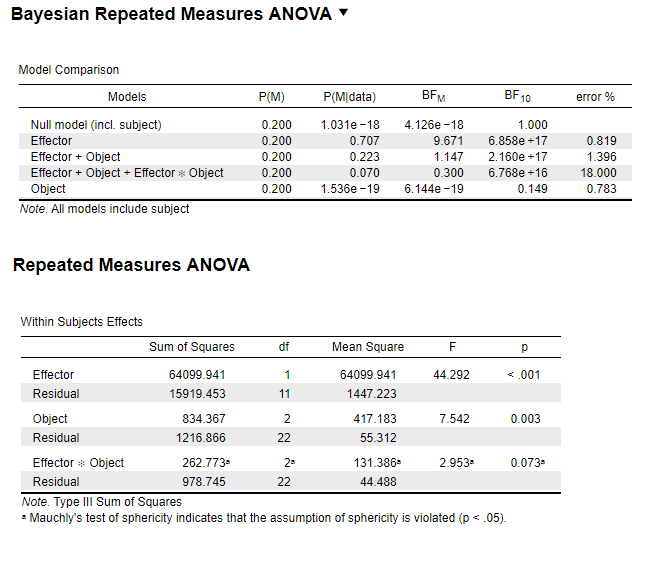
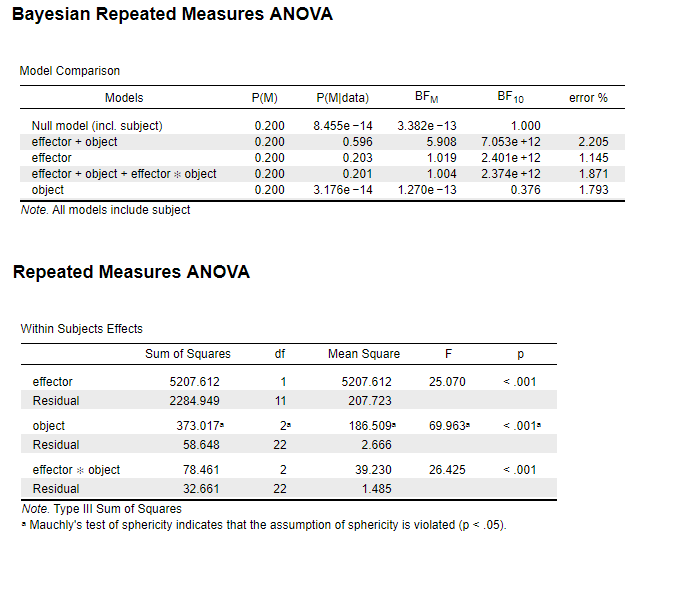
Comments

• EJ

  June 2021

  Hi Yuqi,

  We've come across these kinds of discrepancies before. Usually the Bayesian results are consistent with what you'd get from applying a frequentist linear mixed model to the data (the Bayesian RM ANOVA is really a mixed model). Also, the model comparison works a little different in the frequentist framework, where you test with comparison to the full model. I'm attending some other people from the team to this post, they may have more to say.

  Cheers,

  E.J.
• EJ

  June 2021

  Also, I recommend you update to 0.14.1 :-)
• yuqi

  June 2021

  Hi E.J.

  Thanks for your feedback. I ran the same analyses in 0.14.1 and got the same results. In cases of such large discrepancy, how should I interpret and report the results in papers? I appreciate if anyone from your team can help with this!

  Also, can you explain more, or point to me any documents, about how model comparisons are done differently between the frequentist and the Bayesian framework?

  Thanks,

  Yuqi
• JohnnyB

  June 2021

  Hi Yuqi,

  The project that EJ referenced is available as a preprint here: https://psyarxiv.com/y65h8/

  We are currently working on expanding this to a special issue, with a discussion on best practices in Bayesian mixed model comparison. We have noticed that results between JASP/BayesFactor and p-values occurs when here are strong random effects present in the data (so for instance, your participants responding very differently to manipulation of your "effector" variable). It is hard giving a clear answer without access to the full data set. So if you want to email it to me (j dot b dot vandoorn at uva dot nl), I can take a closer look and give a more extensive answer.

  Cheers

  Johnny
• yuqi

  June 2021

  Hi Johnny,

  Thank you! I will send the data to your email.

  And I have a follow-up question. It's less a concern for t-tests because there are no mixed models involved, correct?

  Thank you for your help,

  Yuqi
• Myrthe

  August 2021

  Hi all,

  I am currently facing the same issue, my bayesian results are completely different from my rm-ANOVA results where I analyse a 3 x 2 x 2 fully within-subject design. I am having a really difficult time deciding how to procede as these two different approach would lead me to conclude very different things.

  Interestingly however, the bayesian results are very much in line with the results of a linear mixed model (using lme4) where I only add a random intercept for participants (y ~ a*b*c + (1|ID). However, I read that a LMM model without random slopes can lead to very high type 1 errors so these slopes should be fitted whenever possible (even for aggregated data; Brauer & Curtin, 2017). Since my data seems to include a lot of random variation, this makes me a bit suspicious of the bayesian anova results, as it seems that,this is similar to an intercept only model and might therefore not be reliable. For example, if I fit the following model to my (aggregated) data: y ~ a*b*c + (a*b | ID) + (b*c| ID) + (a*c| ID), the results are very much comparable to the frequentist rm anova results (here I only omitted a slope for the highest level interaction as this is not possible with aggregated data).

  I am wondering what your thoughts on this are and what you how you would recommend to go about.

  Thanks a lot in advance!!

  Myrthe
• EJ

  August 2021

  Hi Myrthe

  1. Yes, we generally also find that the Bayesian results are more in line with the frequentist results from lme4.
  2. In the preprint that Johnny mentioned you'll see a discussion of adding those random slopes. I agree with you that these models are worth including.

  Cheers,

  E.J.