Evidence for interaction in Bayesian RM ANOVA
Hi, I would like to ask regarding the optimal analysis for interaction (within-by-within) term of two main factors. In particular, I would like to better understand how to estimate BFincl for the interaction and thus whether the effects should be calculated "Across all models" or "Across matched models".
As far as I understand, "matched models" should be preferred to evaluate the interaction term, since this strips the possible influences of main effects. For example, if I have 2 main factors (A,B) +1 interaction, the "matched models" allows me to estimate BFincl by comparing a model (A+B) against (A+B+A*B), thus to evaluate the evidence for (or "additive value" of) the interaction term. Is it correct that one should estimate matched models to get the BF estimate for the interaction term (ad least when the model is relatively simple)? Or is there a situation when "across all models" should be preferred for interaction terms?
Secondarily, following the same rationale, should "matched models" be also preferred for main effects?
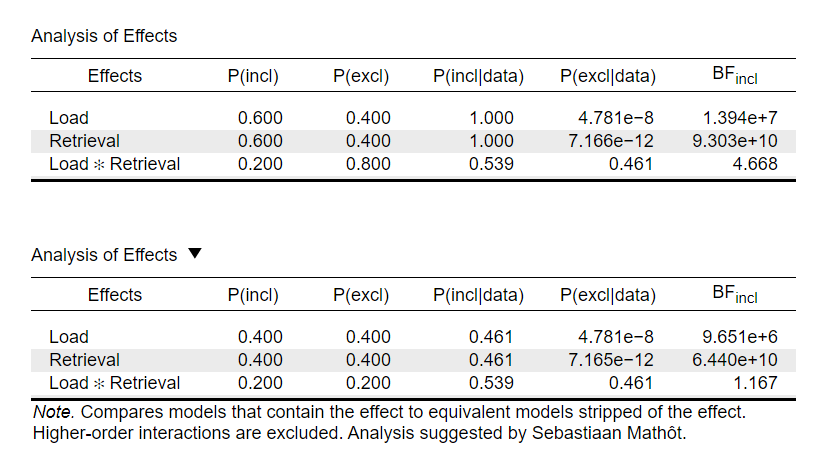
I attended the latest JASP Bayesian workshop and did not notice this option, at least not realizing it may be that important to ask about it in more detail, so I hope I can get a kind of beginner-friendly response here. The thing is that reviewers of our paper asked to perform BF for RM ANOVA and "all models" versus "matched models" selection makes a difference (BF incl = 4.67 versus 1.17), i.e., while the former analysis of effects suggest moderate evidence (thus warranting a further investigation), the later suggests absence of evidence (please see the results below).
Thank you for your help,
MM


Comments
Hi Martin,
That's a good question. Unfortunately, there is no immediate "correct" answer, but rather there are two trains of thought. Originally inclusion probabilities (and thus inclusion Bayes factors) were computed by considering all models with an effect and pitting those against all models without that effect. The original approach is very sensible as long as there are no interactions, but when there are interactions then things get a bit odd. See the post by Sebastian Mathot which discusses this in-depth, and which lead to matched models being implemented in JASP (https://www.cogsci.nl/blog/interpreting-bayesian-repeated-measures-in-jasp). It's worthwhile to point out that the two approaches are identical when there are no interaction effects.
I personally prefer matched models as I find the competing sets of models more sensible, both for main effects and for interaction effects. However, I should point out that there is, as far as I know, no theory/ statistical literature that properly compares the two approaches, so I do not have any references to back up my position.
About your scenario specifically,
For example, if I have 2 main factors (A,B) +1 interaction, the "matched models" allows me to estimate BFincl by comparing a model (A+B) against (A+B+A*B), thus to evaluate the evidence for (or "additive value" of) the interaction term. Is it correct that one should estimate matched models to get the BF estimate for the interaction term (ad least when the model is relatively simple)?
That is correct, in this case the matched models approach compares A+B+A*B to A+B, which is essentially a direct comparison of two models and the inclusion BF is identical to the Bayes factor that directly compares the two models.
Or is there a situation when "across all models" should be preferred for interaction terms?
In this example, "matched models" shows the benefit of including the interaction over just the two main effects. "Across all models" pits the one model with the interaction effect against all other models, which is a very different comparison. In your case, I think that the matched models approach is more appropriate. In general, it really depends on the question you want to answer.
I hope that answers your questions!
Cheers,
Don
Thank you Don,
I really appreciate your response, reference, and support your team provides! It's just amazing!
Best, M.