Understanding "Main and Interaction Effects" in Bayesian ANOVA
Hello everyone,
I have a question on the analyses that I am currently trying to run in JASP. I will limit myself to one example which should then help me coping with the rest.
So, I have a mixed-factors design with one repeated measures factor (scenario, three levels) and one between-subjects factor (Studiennr, 6 levels). I am mostly interested in an effect of Studiennr, i.e., I expect data to show differences across the different studies, and I expect interaction effects of Studiennr and scenario. The results in JASP (default priors) give me the following:
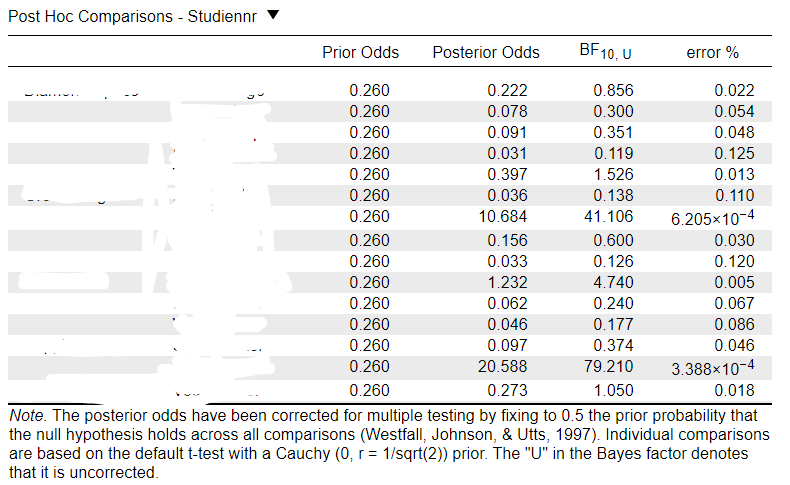
Sorry for blurring the post-hoc tests.
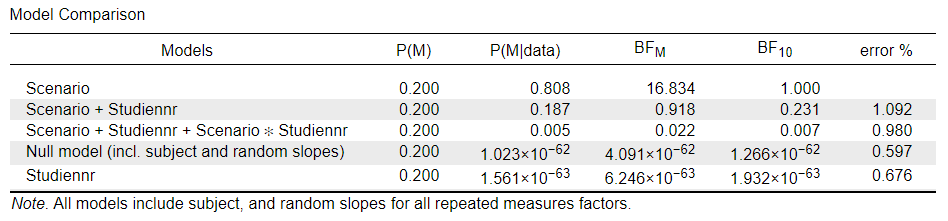
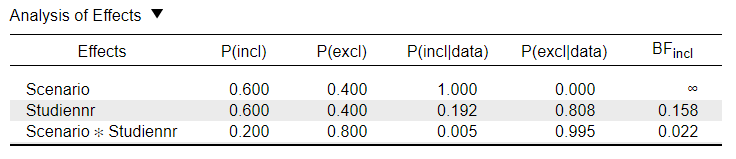
I have been trying to interpret the results and find the correct reporting following https://www.cairn.info/revue-l-annee-psychologique-2020-1-page-73.htm (I understood that I can use BFincl in analysis of effects to determine whether there are significant effects of the factors scenario, Studiennr, and interaction. If BFincl >3, I would assume an effect - please correct me if I'm wrong.) .
If I understand things correctly, the Model Comparison Table indicates that the model only including scenario is the best predicting. Also, considering the Table "Analysis of Effects", it seems like while the scenario most definetely has an influence (BFincl = infinity), the posterior probability of the data decreases both for including the main effect of scenario and the interaction effect.
However, I am not sure whether I correctly interpret the data for the following reasons
a) a frequentist analysis reveals significant main effects of scenario and Studiennr and a significant interaction
b) the descriptives look very much like there is an effect of Studiennr
c) the post hoc tests indicates differences across some of the levels in Studiennr (e.g., 7th line, 14th line).
I would greatly appreciate if someone could help me understand the issues at hand - while there is lots of stuff on t-tests, I still find it hard to cope with the Bayesian ANOVA...
Best regards,
C


Comments
Dear C,
You are interpreting the output correctly. The discrepancy to the frequentist result worries me a little and I'd like to get to the bottom of it. Did you use our latest ANOVA implementation? (see https://jasp-stats.org/2022/07/29/bayesian-repeated-measures-anova-an-updated-methodology-implemented-in-jasp/)
Cheers,
E.J.
Hi E.J.,
thanks for the reply. I am using JASP 0.16.4 - therefore yes, should be the latest implementation. I've been trying some more stuff, maybe helpful for you to understand what's happening.
Here's the result of the equivalent parametric ANOVA:
Sorry, again I must blur the levels. I can see that effects are considerably small and the level of significance is not that far from the magic p = .05 and I've read that Bayes in such cases often only provides anecdotal evidence, however Bayes in this case was even below 1, indicating that the observed results are less likely to occur when including Studiennr as a predictor. If anecdotal evidence, it would therefore be for the null effect.
Also, in the frequentist ANOVA the effect calculation would be based the effect square sums, I therefore dared to just average over the four points of measurement, re-calculating an ANOVA with only one value per person with the between-subjects factor Studiennr only, as for calculating the main effect, the ANOVA method anyways pretty much does the same.
The Bayes ANOVA still provides different results compared to the frequentist:
I therefore assume the source of the discrepancy is in the between-subjects calculation?
Best regards,
C
With your sample size and design, I am not surprised that p=.041 maps on to BF01 = 10/6. I'll ask other team members about this and see what they say.
Cheers,
E.J.
I wonder if this discrepencies may also be related to the different model comparisons that the frequentist and Bayesian ANOVA do by default. This could be the case if, (1.) you used the default settings for both analyses (which are not equivalent), and (2.) if the number of subjects varies across the different levels of the between-subject factor (Studiennr). I can see that you used the default Type III sums-of-squares in the frequentist ANOVA and the set of models used for the Bayesian ANOVA is the Type II set. If you use the same settings for both analyses, do you see better agreement between the results?