One-sided Bayesian t test with the BayesFactor package - How to get posterior of d?
Hi,
I am trying to replicate the one-sided Bayesian t test from JASP with the BayesFactor package in R. To get the posterior of d, I use:
bf <- ttestBF(formula = Variable1 ~ Variable2, data = mydata)
bf
chains = posterior(bf, iterations = 1000000)
summary(chains)
median(chains[,4])
This gives me the median of the posterior of the effect size, right?
However, if I use a one-sided test:
bf.signed = ttestBF(formula = Variable1 ~ Variable2, data = mydata, nullInterval = c(Inf, 0))
bf.signed
chains = posterior(bf.signed, iterations = 1000000)
summary(chains)
median(chains[,4])
R produces the following error:
chains = posterior(bf.signed, iterations = 1000000)
Error in posterior(bf.signed, iterations = 1e+06) : Index argument required for posterior with multiple numerators.
I don't know why this happens, because the two bf objects (bf, bf.signed) look identical to me. Does anyone know how the get the median d in a one-sided test?
Moritz


Comments
Hi Moritz,
I would apply the two-sided test and then toss out all the negative values for d.
Cheers,
E.J.
Hi EJ,
thanks, I tried that out. I used
median d for one-sided test
median(chains[,4][chains[,4]>0])
for that. However, in some cases a really unrealistic high value for d is estimated. I attached an example here https://syncandshare.lrz.de/dl/fiBV1uWpk5kvu2xkKdZDUS1o/onesidedBF.rar
The descriptives are
Low Mean 3.17 SD 0.54
Hig hMean 3.19 SD 0.35
which gives a conventional d of d = 0.03
Without the negative values, d = 0.17 is estimated, in JASP the value is even d = 0.195
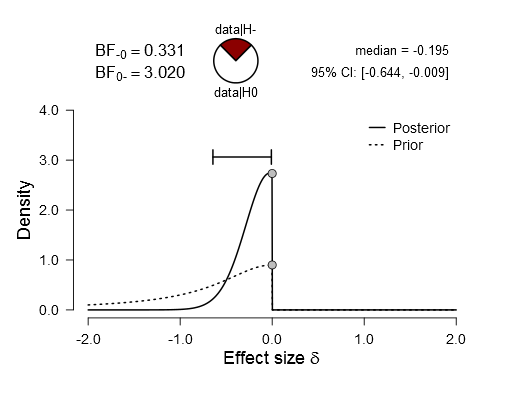
In other cases, the one sided d is closer to the two sided value. I really do not know what to make out of that.
Sure but this makes sense, right? If you look at the mode, it should be near zero. But the median is the 50% cut-off point, so creating a one-sided test makes a big difference. So it is not unrealistically high. It is just that with a non-symmetric distribution, you don't want to summarize with a single point. Looking at the entire distribution is better, imo.
E.J.
Want do you think of reporting the one-sided BF and the "two-sided" normal d? (of course, annotating that)
Yes, that is exactly my preferred way of reporting the results!
E.J.