Informed Prior Bayesian Paired Samples t-test
Hi,
Using a simple effect revealed in Experiment 1, I want to know the strength of evidence for this effect being replicated in Experiment 2 (two separate experiments where Exp2 is a direct replication of Exp1). To do so, would it be justified to use the Bayesian Paired Samples t-test with an informed Prior based on the effect size (Cohens d) and std from Experiment 1?
More specifically: The Cohen's d of the effect of interest from Exp 1 is 0.4 with std=0.07. Can I use these values to inform the prior (selecting Informed prior, normal) for the Bayesian Paired Samples t-test in Exp2?
When I try this, I obtain the following output for Experiment 2:
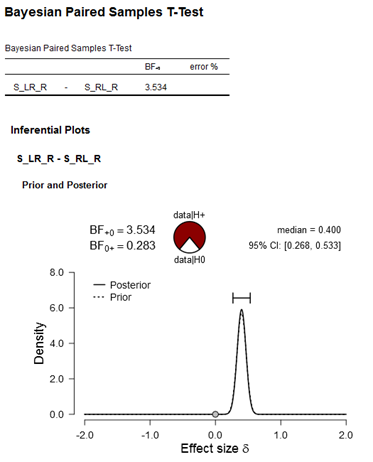 Figure: Bayesian Paired Samples T-Test. Input in JASP: ConditionA(S_LR_R) vs. ConditionB(S_RL_R); Hypothesis (Measure 1>Measure 2; my expected direction of the effect), Bayes Factor: BF10, Informed Prior (effect size 0.4, std 0.07, which is the effect obtained in Exp1).
Figure: Bayesian Paired Samples T-Test. Input in JASP: ConditionA(S_LR_R) vs. ConditionB(S_RL_R); Hypothesis (Measure 1>Measure 2; my expected direction of the effect), Bayes Factor: BF10, Informed Prior (effect size 0.4, std 0.07, which is the effect obtained in Exp1).
My conclusion here would be I have anecdotal/moderate evidence for data|H+ (i.e., anecdotal/moderate evidence for a replication of my previous effect revealed in Exp1).
Many thanks for your help. I am very new to Bayesian analysis and reading through other posts about the prior, I am still confused. But I would like understand and use it appropriately, so your feedback is much appreciated.







Comments
Dear MMA,
What you are looking for is a "replication Bayes factor" (Verhagen & Wagenmakers, 2014) -- in other words, the change in evidence brought about by the data from the replication, having updated the prior distribution based on the results from the original experiment.
1. Yes, I agree you need to use the informed prior distribution
2. Instead of using the sample-based information, I would use the posterior after the original experiment. So analyze the data from the original experiment with the default prior, and consider the posterior. Then, for the analysis of the replication, specify a normal prior that closely resembles that posterior.
Cheers,
E.J.
Dear EJ,
Many thanks for your quick reply and the paper is very useful. I now understand the concept of using the posterior after the original experiment as the prior for the replication experiment.
A question that remains unclear to me, is where can I find the exact values (or vector) that underlies the posterior distribution of the original data (Experiment 1), so I can extract the mean and std of that posterior distribution to specify the normal informed prior for the analysis of the replication?
See below, showing the original experiment with the default prior:
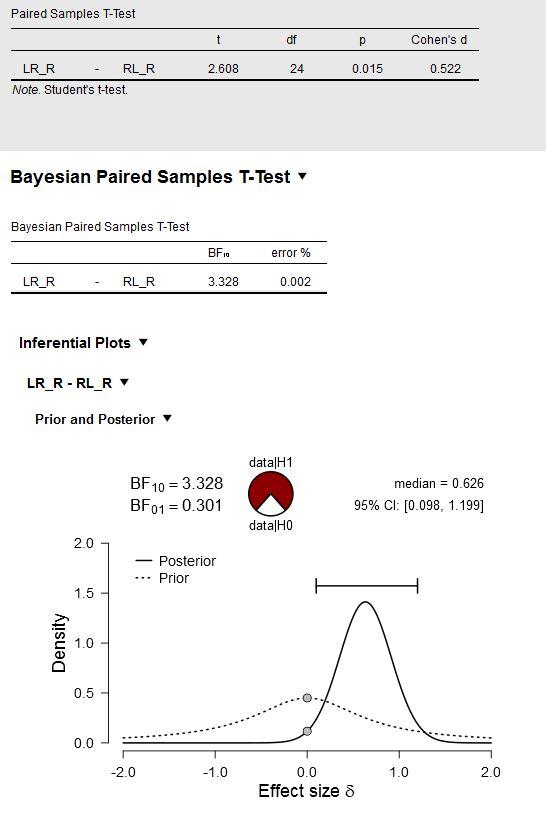
Where can I extract (in JASP?) the values (mean, std) of this posterior distribution (shown above) to specify the informed prior for the analysis of the replication?
Thank you again for your input.
Hi MMA,
Well, the posterior distribution is not exactly a Gaussian (it is close, but for low-N it will have thicker tails). But from the median (=the mean if the distribution is Gaussian) and the 95% CI you can compute the SD.
Cheers,
E.J.
Hi MMA,
Please see the R-code below, it computes the standard deviation of the posterior, based on the difference between the posterior median and the upper or lower value of your credible interval:
For your case, this becomes
Note that this is an approximation, but for the purpose of specifying an informed normal prior this will do just fine!
Kind regards,
Johnny
This post has been very helpful for me. So if I understand this correctly...i can take the posterior distribution from a previous study similar to the one I am currently doing and use that as my new prior.
i.e. use the median from their posterior distribution as the "mean" and the approximated SD from formula as the "SD" in the informed prior tab [normal selection]?
Yes.
Thanks