agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games
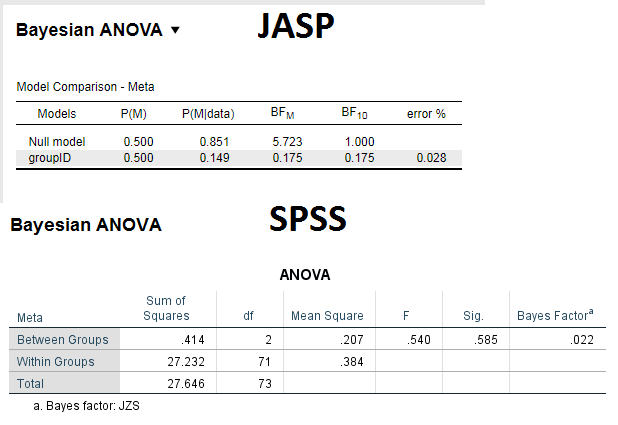







Comments
Dear Vadim,
Cheers,
E.J.
SPSS is in error, almost surely. It would require a prior scale of almost two to get that low a Bayes factor.
Here's my check. This isn't exactly right, because it appears you have slightly different numbers in each group, but this is the only way I can just use the F statistic. It should be very close.
Thank you very much for your answers and great software!
Hello everyone,
First, many thanks to the JASP team for the amazing job! I have the following naive question
For a study we did 4 one-way Bayesian ANOVAs (for 4 different tasks) for both Reaction times and Accuracies. For the Acc the BF10 and 01 are easy to interpret (meaning that there is clear support either for BF10 or BF01), but for the RTs both the BF01 and BF10 are negligible (less than 1). So my question is: when both BFs are less than 1 would it be correct statement to say that the data (in this case the RT data) is not informative ( probably more evidence is needed) and thus no reliable conclusion can be provided by from this data? Or some other way to handle such small BF10 and BF01?
Thank you in advance!
Hi Mila,
BF10 = 1/BF01, so if BF10 < 1 then BF01 > 1. In other words, it is impossible that both BF10 and BF01 are lower than 1, unless you are referring to different tests. Maybe you have a concrete example? In general, BFs near 1 are not diagnostic, at least not as far as the hypotheses are concerned that you are testing.
Cheers,
E.J.
Thanks for the response. Indeed, you are right I dis not express muself correctly. What I was wondering was wheter for cases like BF10 = 0.956 and BF01 = 1.046, for example, where both BFs are not diagnostic, as you said, would be sufficient to say that the data is not sensitive with respect to hypotheses tested and refrain from any conclusions?
Thanks again!
Hi Mila,
Yes. The correct conclusion is that the data do not provide information: the hypotheses under consideration predicted the data about equally well. Of course, the data may be informative in other ways; for instance, perhaps the posterior distribution is relatively peaked, or perhaps most posterior mass is on positive values of effect size, etc.
Cheers,
E.J.
Many thanks!