agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games







Comments
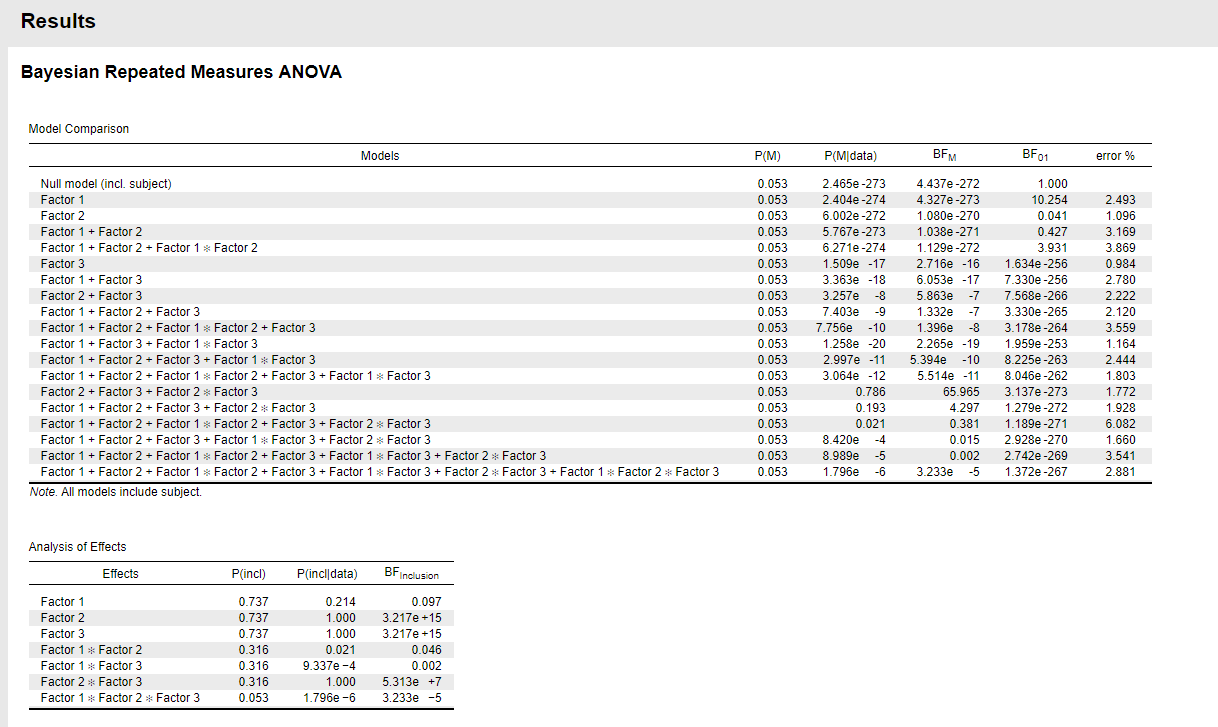
With a large `N`, a small effect (almost 0) might be "nearly significant", but in a Bayesian framework such a small effect with a large N would more indicative of `H0` being true.
Also note that the null model and the factor1-only model are both doing very poorly. So here it would be more informative to look at the inclusion BF for factor 1, which also takes into account more plausible models. As you can see though, the inclusion probability decreases from 0.737 to 0.214, and the inclusion BF is about 10 against including that factor. As MSB says, one explanation for the discrepancy can be a very large sample size. Another issue to look into is violation of model assumption (heterogeneity of variances, structure in the residuals).
Cheers,
E.J.