Repeated Measures ANOVA - post hoc?
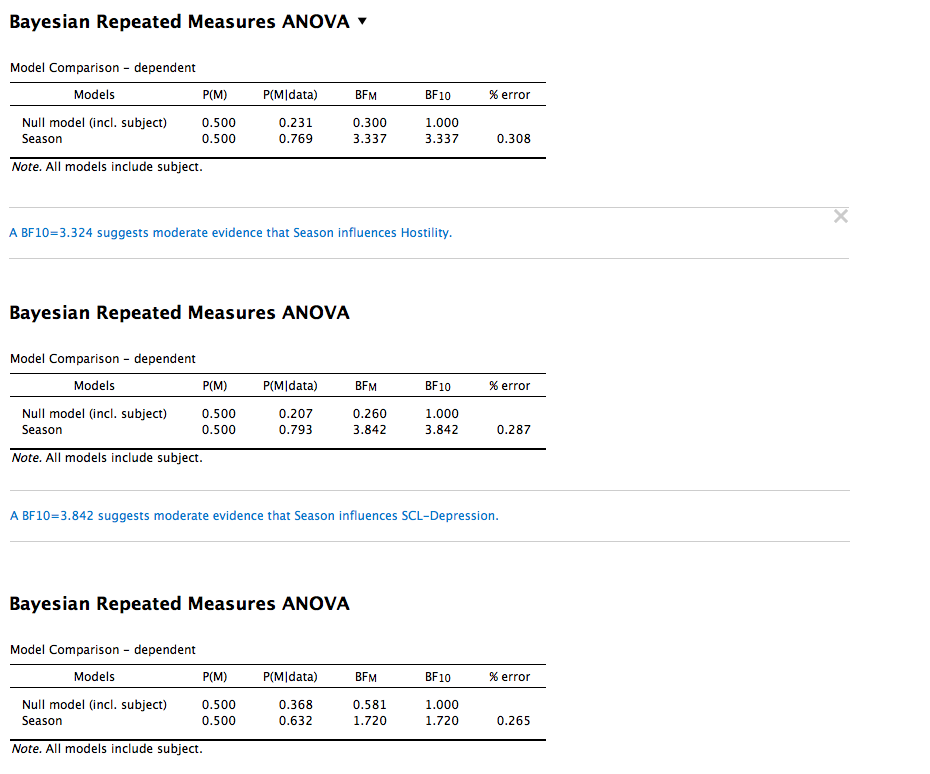
Hello everyone,
I've attached my first output below and I have a few questions.
Brief background: I'm looking at people who spent a whole year at an isolated polar research station, in this output 9/11 crew members participated. They gave me questionnaires at five times: after arrival, autumn, winter, spring, summer.
In the output, you can see that three domains were influenced by season.
Is the way my notes in the output are written the way you would report it in a paper?
What else would I report?
How do I comment on any differences between the five times? Or do I not "need" to?
Are the JASP default Cauchy priors here appropriate to use?
Many thanks in advance,
eniseg the newbie ![]()


Comments
You can look at Part II (https://osf.io/m6bi8/) for some examples. I think this is OK. But I would certainly plot the data!
E.J.
Hi EJ,
thank you so much! I did look at Part II, that's what I was basing my learning of JASP on.
For this analysis I was looking at the Disgust & Fright ANOVA because I couldn't find a "pure" Repeated Measures ANOVA without any interactions/between-subjects factors.
But on p. 21 in Part II, it says "both Bayes factors are barely worth a mention" and mentions 2.6 and 1.5 BF which I can't find in Figure 14. The Analysis of Effects has Digust * Fright = 1.507, but where does the 2.6 come from?
I would have plotted the data either as a bar chart or a line diagram displaying the means of Confusion in each Time, was that what you meant?
Thank you so much for the fast response
About that 2.6: "The model that receives the most support against the Null model is the two main eects model, Disgust + Fright. Adding the interaction decreases the degree of this support by a factor of 3.240=1.245 = 2.6. This is the Bayes factor in favor of the two main effects model versus the model that also includes the interaction." And yes, some visual representation of the means would help to interpret the data.
Cheers,
E.J.