Bayesian RM ANOVA (mixed factorial design) with small sample sizes

CHei

Hi there,

In my experiment, a reaction time task with 2 conditions, I have tested 3 groups (N=22, N=23, N=21).

I am using a mixed factorial design and have run a Bayesian Repeated Measures ANOVA to find out whether performance in the task depends on condition and group (Repeated Measures Cells = Condition 1, Condition 2; Between-Subject Factors = Group).

My questions are:
1) Can I use this analysis with such sample sizes?
2) Right now, I have kept the default prior of 0.5 for "r scale fixed effects" as there isn’t previous research in this area using this task and/or conditions . I assume that by using the default prior, JASP assumes that I'm testing for medium-size effects of 'condition' and 'group'?

Here is the main output table from JASP:

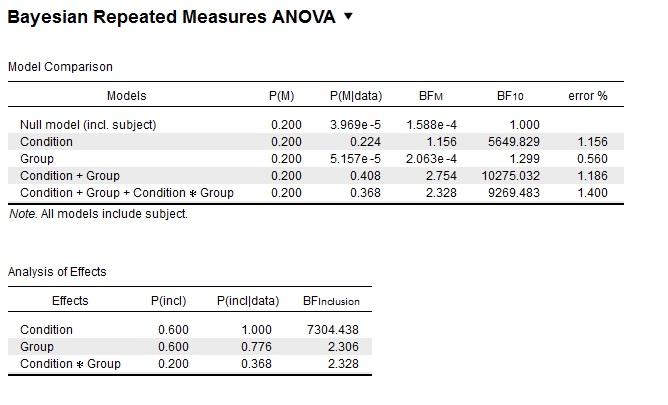
3) Am I right to assume that there is strong evidence for a main effect of condition, but that the BF of around 1 for group can be regarded as noise / data are insensitive? Furthermore, there is no evidence for or against an interaction (for interaction = 0.9; against = 1.11)? Given that the main effect of group does not add much improvement compared to the null model, I think I need to go with the model with just 'condition' as a main effect. However, when I select "Compare to best model", then there is the main effects model (condition + group) on the very top. Does that mean the best model is actually the one with both main effects despite the fact that 'group' doesn't add much improvement?
Here is the "Compare to best model" table:

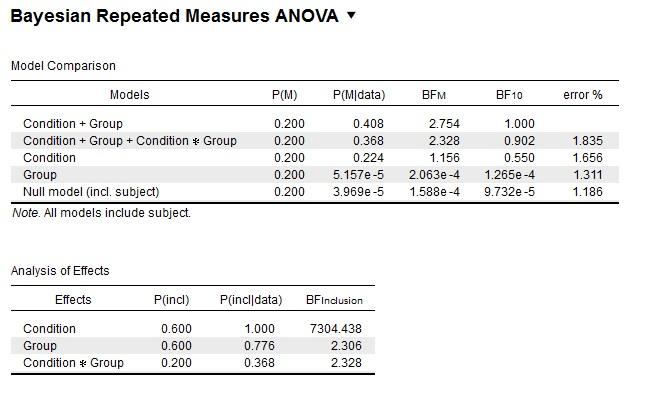
Thanks a lot for any advice!

Aram

Hello CHei,

If I were you I'd wait for E.J. to answer because I'm new to Bayesian inference, but let me tell you what I think.

1. I think you can use this analysis with all sample sizes. The problem is that if your effect is too small, you will need a large sample size to find evidence for or against it. Apparently the effect of condition is huge whereas the effect of group is small.
2. What if you adjust your prior and see what happens? You say that you are testing for medium-size effects, but the condition effect is large and the group effect is not.
3. I want to see what they answer for this one! I have no idea.

EJ

Hi CHei & thanks Aram,

You are basically on the right track with all your remarks.
1. Yes you can use the analysis with all sample sizes.
2. I would stick to the default prior.
3. If you select "compare to best model", the resulting BF's are easier to interpret if you also select "BF_01" as the presentation mode. What this will reveal is that the best model is only marginally better than the next two models. This ambivalence is also reflected in the results of the "Effects"; the inclusion BFs are relatively weak when "Group" is involved.

So Condition definitely matters, and there is some evidence in favor of Group, but this evidence is weak.

Cheers,
E.J.

CHei

Hi EJ and Aram,

perfect, thanks a lot for your help. In a classical RM ANOVA, the main effect of Group is significant, so it's great that the BFs put this in perspective.

Cheers,
C