Strange behavior with Bayesian RM-ANOVA
Hi,
I'm using JASP for a while and I think is a really great tool.
I ran both classical and Bayesian 2 ways - RM -ANOVA. by using the the classical analysis I got main effect to one variable ("cong") and I didn't get main effect to the second variable (go_nogo). In addition, I also didn't get interaction.
However, when I ran the Bayesian analysis I got evidence to the existing of the main effect to the second variable go_nogo).
As far as I understand Bayesian statistic, the pattern should be the same. I understand that it possible to find that by using Bayesian analysis effect will disappear, but I'm not really sure how it possible to find different effects.
For being sure that I didn't miss anything, I ran more 2 tests:
- one-way (both classical and Bayesian) RM-ANOVA to the 'cong' variable.
- paired samples t-test (both classical and Bayesian) for the 'go_nogo' task.
The results for these 2 tests were same (at least in the pattern):
There was a different between the levels of the 'cong' variable (F=22.16, p<.001, BF10=21,142.844) and no different found in the go_nogo variable(t=1.385, p=.184, BF01 = .539).
However, the results for the two-way ANOVA (as I described before) in the Bayesian analysis:

is different from the classical one:
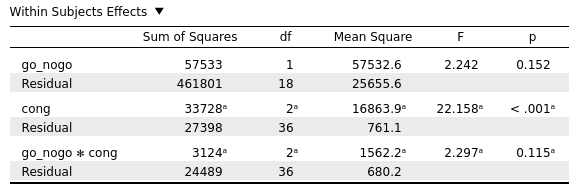
In addition, the "behaviour" of the Bayesian analysis is also different from the results given by the analysis of each variable separately (as given from the one-way ANOVA and from the paired samples t-test)
I can't find any mistake in my steps and I'll really appreciate your comments.
In any case, the jasp file (that includes the latest analysis) is attached as a zip file: https://github.com/jasp-stats/jasp-issues/files/2872991/jasp_inc_ttest_anova.zip
Thanks a lot in advance,
Ronen.


Comments
Hi Ronen,
Looking at the (frequentist) RM-Anova table you provided, that little
'a'marking for the "cong" effect (and its interaction with "go_nogo") indicates your data violation of model assumption of Sphericity. This, in combination with @EJ's comment on another thread, I decided to take a deeper dive into your data in R - and seem to have found the source of the discrepancy (and perhaps the reason this topic is so popular on this forum).In R, I ran a Bayesian RM-Anova, adding random effects for "cong" and "go_nogo" (and their interaction) for each subject. Averaging across the (matched) models, using
BFEffects::inclusionBF(equivalent to the "effects" option in JASP) I found the following:These results are more consistent with the (frequentist) ANOVA table above:
Note that the sudden appearance of the main (fixed) effect for "cong" (
BF10=361,406) seems to be at least partially driven by a lack of a random effect for "cong" (BF01=5.31) this would also drive the RM-Anova towards a significant effect.Likewise, the effect for "goNogo" (
BF10=16.09) seems to be weak perhaps due to large variance in this effect across subject (i.e., a random effect for "goNogo";BF10>1,000,000), which would also push this effect away from significance in the RM-Anova.Now... The model averaging was done across all models (all possible combinations of factors, barring the inclusion of an interaction without its main effects), and I'm not sure if these are the models that should be averaged across. Perhaps @EJ could be of some help in this regard.
Attached is the code and data used for this analysis.
Mattan
As a footnote, the violation of the assumption of Sphericity might also explain why post-hoc t-tests gave such strong results -- as these tests do not have the Sphericity assumption.
Thank you Mattan (@MSB) for your detailed answer - I'm really appreciate your generous help.
However, I'm not really sure what should be the bottom line here. On one hand, by taking into account the frequently used approach suggested by JASP the Bayesian analysis leads to inconsistent conclusions, on the other hand it seems that exclusion of random effects leads to more consistent conclusions but in the same time it seems (at least to me) less accurate.
I'm really confusing about this dissociation between these two approaches and it make me uncomfortable with Bayesian ANOVA (at least as it suggested by JASP).
Please note that my knowledge about all of research area is pretty limited so maybe I'm really miss all the picture here.
I hope that @EJ or somebody else from JASP's teem, has cut and clear answer to this enigma.
Best,
Ronen.
Hi Ronen,
This is a really interesting issue. I think you should also be uncomfortable with the frequentist results, probably. But what seems to be going on here is model misspecification, on more than one level (the sphericity and the random effects structure). I can't say much more now but I'll bring this to the attention of the team.
Cheers,
E.J.
Deer @MSB or deer anyone who can give me some help. :)
Hi, I am truly having great benefit in my current analysis using JASP.
However, I had a similar problem as Ronen did.
To explain my data shortly,
With JASP, I ran RM ANOVA (both frequentist and bayesian) analysis in 2(cue) by 4(size) within subject design.
(Attached file can be found in https://github.com/Minius93/biasSigmaAnal .)
Firstly, I found mismatch between p-value and BF for cue condition. (JASP file).
While p-value for cue condition remain not significant(p=.125), BF show highly significant main effect of cue condition! (BF=63.003). As a reason for such mismatch, I found that the violation of Sphericity can be a problem based on this question and the other question raised by “TooFred ” (https://forum.cogsci.nl/discussion/4073/testing-assumptions-for-bayesian-repeated-measure-anova)
However, unlike RM-ANOVA, Bayesian RM-ANOVA does not have option for correcting such violation in JASP.
Then, I saw the answer you provided to Ronen, it seems somehow violation of Sphericity is related to the random effect. I though my unreasonably high BF can be explained by random effect (cue:ID).
As you stated above, I ran the same Bayesian RM-ANOVA with R (BFEffects) with my data, which is also attached within Github (R). The result is like the figure…
As you see, there was high BF in cue condition and also very high BF in cue:ID random effect condition.
In such case, Is it possible to say that the unreasonably high BF I found in JASP is driven by random effect?
If such statement is correct,
Would you recommend any references suggesting relation between violation of Sphericity and random effect?
Thank you so much for providing such a useful tool and hope you have a great day!
Yong Min Choi
This suggests some actual statistical research; we'll look into it
E.J.