Inconsistency between frequentist and Bayesian RM ANOVA (or I've run the latter incorrectly)

JLeborgne

Hello. Maybe this is a silly question, but I couldn't find consistent answers neither from the internet nor from colleagues. Thanks in advance!

I've run a regular RM ANOVA in SPSS with 3 factors (2x2x7 design). I did not find a significant main effect of the factor 1 (p = 0.066). However, we all know this isn't conclusive so I decided to ran a Bayesian RM ANOVA to see to what extent the data supports the null hypothesis in relation to that particular factor, assuming that H0 means that there's no difference between both its levels.

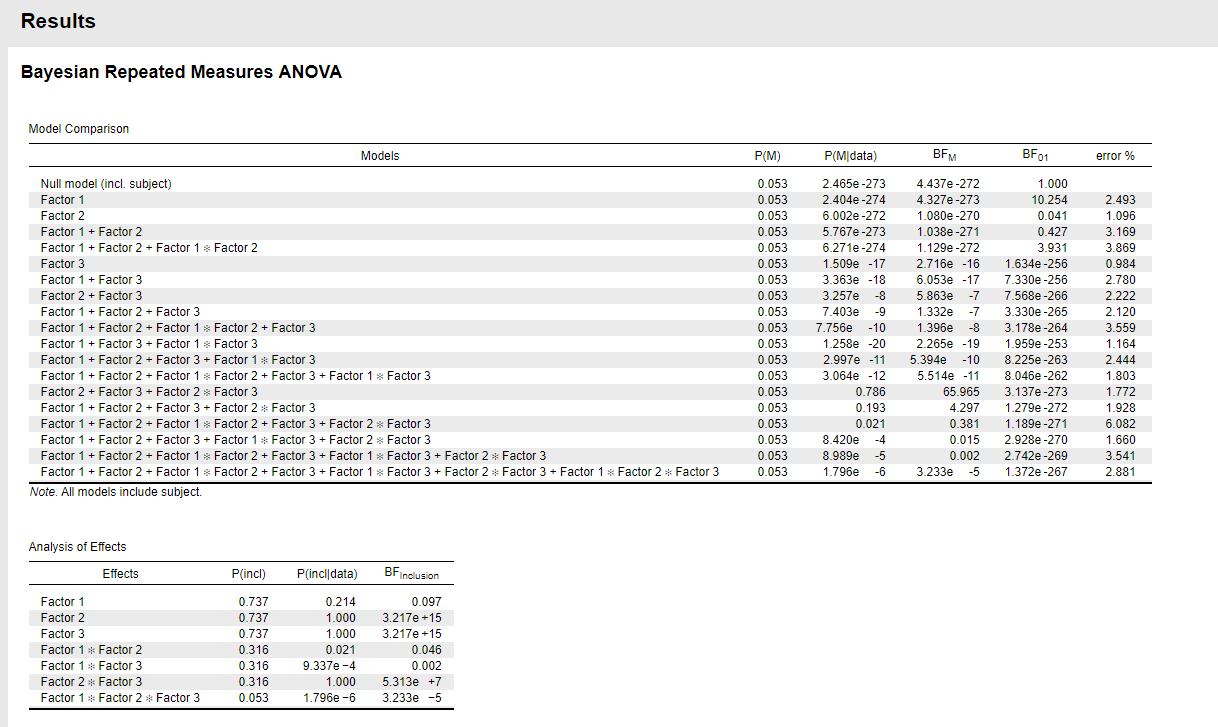
The Bayesian RM ANOVA in JASP gives me a BF10 of 0.098 and a BF01 of 10.254 (see image below), hence strong evidence in support of the null hypothesis. However, I was told that this isn't feasible when you got a p-value of 0.066 for an effect of said factor because my p-value suggests 1 in 18 chances of getting data this extreme under the null hypothesis whereas the BF implies that the data are 10 times more likely under the null than the alternative hypothesis.

What do you think is the problem? Do you think I'm making a mistake in the way I'm calculating the BFs? I'm certain that the frequentist RM ANOVA was well done.

MSB

With a large `N`, a small effect (almost 0) might be "nearly significant", but in a Bayesian framework such a small effect with a large N would more indicative of `H0` being true.

EJ

Also note that the null model and the factor1-only model are both doing very poorly. So here it would be more informative to look at the inclusion BF for factor 1, which also takes into account more plausible models. As you can see though, the inclusion probability decreases from 0.737 to 0.214, and the inclusion BF is about 10 against including that factor. As MSB says, one explanation for the discrepancy can be a very large sample size. Another issue to look into is violation of model assumption (heterogeneity of variances, structure in the residuals).

Cheers,

E.J.