Repeated factorial mixed anova
I would like to do a Bayesian repeated factorial mixed anova analysis. My study involves a treatment condition vs a placebo condition (main effect: condition) and measurement before and after treatment (main effect: time). My Ha is that there is an interaction effect vs H0 there is no effect.
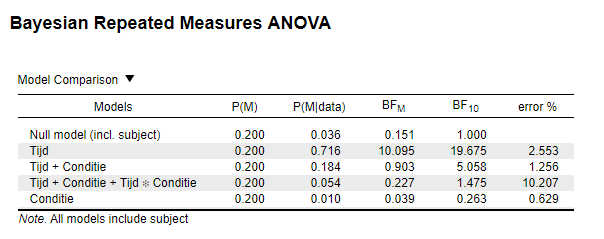
The output of JASP is the following:
I read that through transitivity you could make the statement that there is moderate evidence against an interaction effect by dividing BF10 of Tijd + Conditie + Tijd * Conditie (1.475) by BF10 of Tijd + Conditie (5.058) = 0.29. Is that a correct interpretation?
Next to that, if I would like to say something about the likelihood of the null-model vs the interaction effect. Is that possible and how should I calculate that?
Best regards,
Ellen


Comments
Hi Ellen,
Hf = full model (with interaction); Hm = main effects only model; H0 = null model
BFf0 = 1.475; BFm0 = 5.058
BFf0 * BF0m = BFfm, or
BFf0 / BFm0 = BFfm, meaning
1.475 / 5.058 = BFfm = 0.29, so data are about 1/0.29 = 3.45 times more likely under the main-effect model than under the model that adds the interaction. So: you are correct.
If you compare the model with no factor in there at all to the full model, you see that the data are only somewhat more likely (1.475 times more likely) under the full model. Overall, I'd say that the data suggest there is a main effect of time, but not much else.
E.J.