Post-hoc comparisons for Bayesian mixed ANOVA
Hey.
I have some unclarities regarding post-hoc comparisons for a Bayesian mixed ANOVA. I have two factors: the between factor age (young and old) and the within factor set size (24, 48, 72 and 96 words per set). A classical ANOVA yields a significant main effect of age and set size on the hit reaction time; the interaction is not significant. The Bayesian analysis agrees with these results: there is extreme evidence for including age and set size as factors and also substantial evidence to not include the interaction.
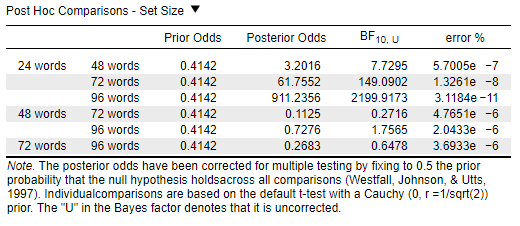
Since there is a significant effect of age, I want to do post hoc comparisons for each of the age groups. This means I will do 12 comparisons, 6 for the young participants and 6 for the old participants (see table below, both for young and old participants). There seems to be no option to do this in JASP (or none that I found/understood). To achieve this, I would split my data set by age group and calcluate simple Bayesian repeated measures ANOVAs and their post hoc tests.
My problem is: how exactly do I control for multiple comparisons in this case. Normally, this is done by fixing the prior odds to 0.5. If I followed van den Bergh et al. (2019) correctly, the adjusted prior odds are calculated as follows:
(1) p(H0) = 0,5; number of conditions = J = 8 (2*4, since there are 4 set size conditons and 2 age conditions, resulting in 8 data cells)
(2) tau² = p(H0) ^ (2/J) = 0,5 ^ (2/8) = 0,8409
(3) adjusted prior odds = (1 - tau²) / tau² = (1 - 0,8409) / 0,8409 = 0,1892
(4) posterior odds = BF10U * prior Odds
This method seems to be rather conservative, dividing the Bayes factor by a factor of 5. Am I overcorrecting? Is there an other way of doing this? Im greatfull for any input.
I also have trouble on finding a source on how to interpret the posterior odds. Are they interpreted in the same way as a Bayes factor? In their paper, van den Bergh et al. (2019) simply refer to posterior odds of 16, 23 and 27 as "evidence" and huge posterior odds (e.g. 1,04 x 10^9) as overwhelming evidence. This seems to differ from the standard Bayes factor interpretation.
I am extremly gratefull for any help, since I seem to have exhausted all the usual guides (JASP guide paper, Wagenmakers et al. 2018...).
Cheers
Pete




Comments
Hi Pete,
First and foremost, here is a thesis that summarizes some of this work: https://psyarxiv.com/s56mk
Second, I was a little confused about how many conditions you have -- you say "This means I will do 12 comparisons, 6 for the young participants and 6 for the old participants " but later you say "number of conditions = J = 8 (2*4, since there are 4 set size conditions and 2 age conditions, resulting in 8 data cells)"
Third, you can check your results with those in the JASP output (I see 6 comparisons, however, in that table). I haven't checked but the kind of correction you mention seems about right. It is after all a kind of Bonferroni-type correction.
Fourth, posterior odds reflect belief, plausibility, or intensity of conviction; a Bayes factor reflects relative predictive performance -- therefore it is the extent to which the data change the beliefs/plausibilities/intensities of conviction.
Hope this helps,
Cheers,
E.J.
Hey EJ,
thank you so much for your response.
1. I think the paper is way above my paygrade, but I will give it a try. :)
2. Sorry for the confusion, I will try to clear things up. I think it has to do with the fact that I don't quite understand the control mechanisms for Bayesian post-hoc comparisons.
As I said I have the factor age (2 levels; young and old) and the factor set size (4 levels; 24, 48, 72 and 96 words) and I am investigating the effects of those factors on reaction time. Since there is an age effect, I want to do the post-hoc comparisons for both age groups seperately, resulting in 12 comparisons:
young participants: 24 vs. 48, 24 vs. 72, 24 vs. 96, 48 vs. 72, 48 vs. 96 and 72 vs. 96
old particpants: 24 vs. 48, 24 vs. 72, 24 vs. 96, 48 vs. 72, 48 vs. 96 and 72 vs. 96
For the frequentist ANOVA, I would do Bonferroni adjustment by multiplying the p-value by a factor of 12.
For the bayesian ANOVA, my understanding is, that the post hoc adjustment of the prior odds was based on the number of conditions (young: 24,48,72,96; old: 24,48,72,96), not the number of post hoc comparisons (12, see above). Am I wrong?
In any case, there is no option in JASP (as far as I can tell) to adjust for 12 comparisons since (1) there is no option to do seperate post-hoc comparisons for young/old participants (2) and since the calculation of the prior odds is based on the number of conditions (see van den Bergh et al.,2019; for 5 conditions, there will be 10 post-hoc comparisons, for 6 conditions there will be 15 comparisons and so on)
Since you say that post-hoc comparisons for the Bayesian ANOVA are a kind of Bonferroni-type correction, I would suggest following approximation:
I have been able to approximate the adjusted prior odds using this tool (https://mycurvefit.com/) and a four parameter logistic fit. The fit is quite good (R² = 0,999).
The adjusted prior odds for 12 comparisons would be 0.29. I know this method may not be mathematically correct, but for an approximation it seems to do the job quite well. What do you think?
Thank you again and sorry for the wall of text,
Cheers,
Pete
Edit of above post:
After trying to work my way through the thesis mentioned above I now know that there are two different methods on null control: on based on the number of comparisons (Jeffreys) and one based on the number of conditions (Westfall; which is less conservative).
1) Using Jeffreys approach for 12 post-hoc comparisons I calculated prior odds of 0,12., which seems way conservative to me.
2) Using Westfalls approach for 6 conditions (and consequently 15 comparisons) results in prior odds of 0,26.
3) Using my approximation for 12 comparisons I get prior odds of 0,29.
I'm still very unsure which method to use. My gut tells me to prefer option 3 over option 2 over option 1. What do you think?
---------------------
Also, I am still struggeling on how to tell my reader on how to interpret the adjusted posterior odds. I don't want to go into too much detail explaining Bayesian methods in my thesis (since it should focus on the set size effect, not statistical methods). This is my first time using Bayesian methods, so please bear with me. I know, that the Bayes factor and posterior odds reflect different things. However, the adjusted posterior odds just happen to be the Bayes factor multiplied by a factor to correct for multiple comparisons, pretty much like the Bonferroni correction of a p-value. Therefore I would argue that the adjusted posterior odds can be interpreted in a similar way (for ease of understanding) by using the interpretation guidelines for the Bayes factor (see Wagenmakers & Lee, 2014). Any thoughts on that?
Anyway, thanks for your help!
Cheers,
Pete
Hi Pete,
Hmm yes this is very interesting. This is also an understudied topic. Based purely on pragmatic considerations, I'd recommend option 2: it is based on a published paper, it is close to option 3, and it is used in JASP. You could argue for option 3 but it would be a lot of extra work for almost no benefit, as the prior model probabilities are so similar.
I think your interpretation is fine.
Cheers,
E.J.
Hey E.J.,
thank you again for your input. I agree: it makes sense to base the prior odds on option 2, since it is only off by 0,03 and based a "real" statistical basis.
Another quick question. When correcting the posterior model odds, smaller effects (e.g. BF10, U = 0,5; posterior Odds = 0,13) recieve moderate support for the H0, even when the Bayes Factor is indifferent about the data. It feels a bit weird to argue that there is evidence for no difference between these conditions. With frequent statistics you would argue that no statistical signifcant effect can be found, but you wouln't argue that there is no difference (as evidence for the null cannot be expressed). With Bayes the null correction is biased for the H0 (which, now that I think about it, is what one wants). Still, it does feel a little weird interpreting these results. Any thoughts?
Cheers,
Pete
Hi Pete,
I think it works out, intuitively, if we respect the difference between BF as "evidence coming from the data" and posterior probabilities as "reasonable beliefs after seeing the data". Suppose you have many comparisons or conditions, and no data are yet observed. Then the multiplicity correction implies that your prior belief is that the null holds.
But I do agree that it feels strange if the purpose is to demonstrate evidence for the null. I would argue that, if this is the purpose, then (a) the wording suggests that what is sought is evidence, so BF; (b) the prior belief that the null holds might be too pessimistic, as presumably earlier work made the opposite claim. Besides, in this situation you may not find yourself in the exploratory setting that requires the multiplicity correction.
But -- this is really important stuff that is to some extent understudied. I think the best course of action is to be transparent and report both the evidence, the prior correction factor, and the posterior belief.
Cheers,
E.J.
Hey E.J.,
it is good to now that this matter is somewhat understudied, since I started to doubt myself. As you suggested, I will simply be transparent and report evidence, prior correction factor and posterior belief.
Thank you for all your help!
Cheers,
Pete