Bayesian contingency tables test does not behave like an omnibus test

FlorianB

I have a contingency table for which a Bayes Factor analysis shows no support for differences in the distribution of one categorical variable between different levels of a second categorical variable. However, when analysing a reduced version of the contingency table (with focusing on only two levels of the second variable), the Bayes Factor strongly suggests that distributions differ.

I am surprised by this because I had the understanding that the Bayesian contingency tables test is an omnibus test (similar to ANOVA) where the H0 "all distributions are equal" is tested againt the H1 "at least one distribution is different" (see also discussion here: https://forum.cogsci.nl/discussion/6795/bayesian-chi-square-test). However, then adding additional factor levels should not make such a difference. Am I missing something or can anybody explain why adding more factor levels decreases evidence for H1?

Here is some example data:

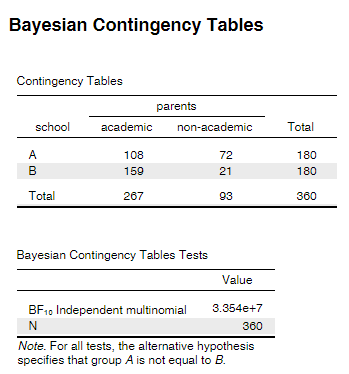
Full contingency table:

Reduced contigency table:

Data file:

exampledata.csv

Thanks a lot!

Florian

FlorianB

for transparency, I have also posted this question here: https://stats.stackexchange.com/questions/553574/why-does-the-contigency-table-bayes-factor-test-does-not-behave-like-an-omnibus

EJ

By adding more levels H1 becomes relatively more complex. The same happens when you quantify evidence for the null in case of data from a fair die. You can either analyze odds vs evens or analyze the uniformity across all categories. H0 will be more strongly supported in the second case, because H1 has so much more flexibility. Of course you could adjust the prior distribution to be more concentrated, and that would counteract this tendency.

E.J.