Bayesian Repeated Measures ANOVA

Mateus

Hi everyone,

I am trying to understand the results of a Bayesian repeated-measures ANOVA.

I want to examine if there is a difference between the two groups (with different subjects) that were tested multiple times for an outcome measure (sprint time). I considered the pre-test, post-test and tapering 1 as "repeated measures factors", the pre-test, post-test and tapering 1 performance as "repeated measure cells", and the groups as "between-subjects factors". In addition, in the main options (order), I select ‘Compare to null model’.

Can you please tell me if my interpretation is correct?

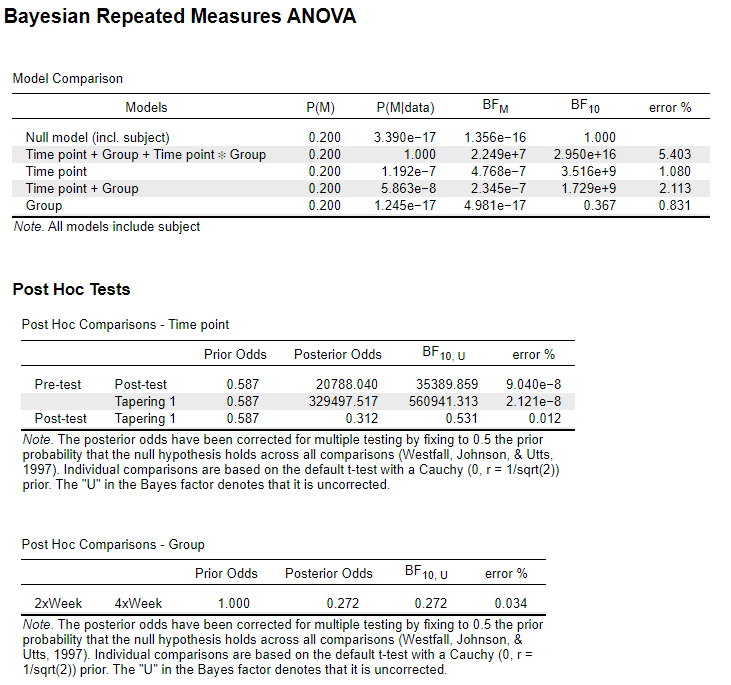
"Using a Bayesian RM ANOVA (prior probabilities of each model were equal to 0.5), the Bayes factor indicates that the data is best represented by a model that included time point as the predictor, the group, and the interaction between the time-point and the group. Post hoc comparisons of pre-test vs. post-test and pre-test vs. tapering 1 revealed posterior odds of 20788.04 and 329497.52 against the null hypothesis, which indicates decisive evidence in favour of the alternative hypothesis. When comparing post-test vs. tapering 1, there was anecdotal evidence in favour of the null hypothesis. Additionally, post-hoc group comparisons exposed posterior odds of 20788.04, indicating moderate evidence in favour of the null hypothesis (no differences between groups)."

Thanks in advance,

Nuno Mateus

EJ

Dear Nuno,

Largely fine; two remarks:

1. " (prior probabilities of each model were equal to 0.5)" -- the BF does not depend on prior probabilities.
2. "Additionally, post-hoc group comparisons exposed posterior odds of 20788.04, indicating moderate evidence in favour of the null hypothesis (no differences between groups)." I assume this is a typo and you mean to refer to the final result? (posterior odds of 0.272)

E.J.

Mateus

Hi EJ,

First of all, thank you for your prompt response and amendments.

I hope I'm not boring you, but can you please tell me if the next interpretation is also correct?

"Using a Bayesian RM ANOVA, the Bayes factor indicates that the data is best represented by the model that just included the group. Post hoc comparisons of pre-test vs. post-test and pre-test vs. tapering 1 revealed posterior odds of 0.256 and 0.749 against the alternative hypothesis, which indicates moderate and anecdotal evidence in favour of the null hypothesis, respectively. When comparing post-test vs. tapering 1, there was moderate evidence in favour of the null hypothesis. Additionally, post-hoc group comparisons exposed posterior odds of 8.51, indicating moderate evidence in favour of the alternative hypothesis (differences between groups)."

Thank you for your patience,

Nuno Mateus

EJ

""Using a Bayesian RM ANOVA, the Bayes factor indicates that the data is best represented by the model that just included the group. "

Yes but the evidence is really weak.

E.J.

Mateus

Hi EJ,

Thank you again. Your suggestion is to just mention the first sentence because the evidence is weak. Am I right?

Regards,

Nuno Mateus

EJ

Your current first sentence may make a naive reader believe that the group-only model ia clearly the best, whereas the data support that model only weakly over the null model.

E.J.

Mateus

Now I understand it!

I agree with you EJ. In the previous format, the sentence could be misleading. 

I rewrote it. Please let me know what you think. 

"Regarding the jump performance, the Bayes factor indicates anecdotal (i.e., weak) evidence that the data is best represented by the model that just included the group."

Thanks in advance,

Nuno Mateus

EJ

yes!

Mateus

Thanks a lot for everything EJ.