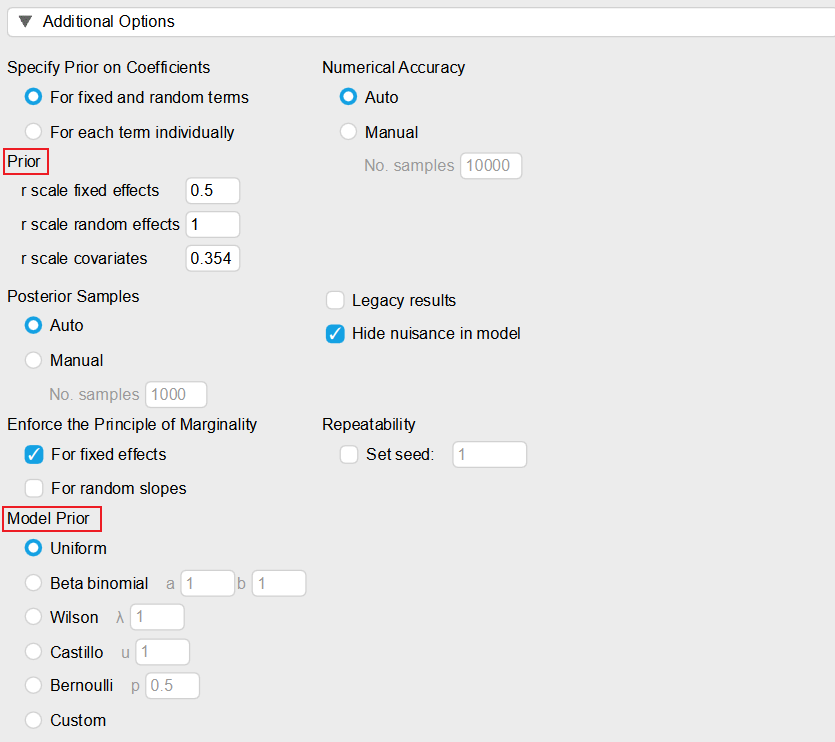
The settings of Prior and Model Prior
Hi JASP team,
I am a novice in Bayesian statistics. Recently, I have explored how to conduct Bayesian ANOVA using JASP and interpret results.
I have a confusion that the distinction or relation between Prior and Model Prior in Additional Options. When I modified the input of Prior, the results of BF10 and BFincl changed, and P(M) did not change. Interestingly, when I modified the Model Prior, the P(M) and BFincl changed, but BF10 had no change. Could you help me to solve this issue?
Moreover, I personally understand the calculation of BF10 is posterior odds divided by prior odds,
and BFincl is
So, the change of BFincl is clear to me, but I am confused that BF10 is influenced by the input of Prior and is not by the input of Model Prior. Generally, Bayes factor is independent of prior probability. I have no idea that the modification of Prior affects BF10, whereas the modification of Model Prior changing P(M) does not affect BF10.
By the way, I use the version 0.16.3 of JASP.
I appreciate you answering my questions!
Best wishes,
Wang


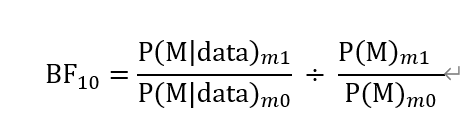
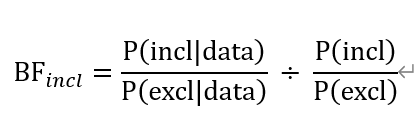
Comments
Dear Wang,
Maybe it would be clearer if we'd use the term "Parameter Prior" instead of "Prior". The parameter prior partly defines the prediction that a model makes, and through these predictions it affects the evidence and therefore the BF01.
On the other hand, the model prior does not affect the evidence, so it leaves BF01 unaffected. To make things more complicated, the inclusion BF with more than two models does depend on the model prior.
Cheers,
E.J.
@EJDear @EJ ,
Thank you for your response!
I have another issue of BF. Recently, I have read your paper titled "Bayesian hypothesis testing for psychologists: A tutorial on the Savage-Dickey method". This paper is meaningful for me to understand the calculation process of BF.
I have understood two methods to estimate marginal likelihood (ML). First, exchanging the role of parameter posterior and ML (see Fig.1). After inputting the result of parameter posterior from MCMC output, the ML can be estimated for two competing models. The BF, in turn, is equal to the ratios of ML of two models (see Fig .2). Therefore, I understand why parameter prior affects BF.
https://forum.cogsci.nl/uploads/265/38PRVARCD4WJ.pngFig .1
https://forum.cogsci.nl/uploads/698/F2BJTBR0A6F2.pngFig .2
Second, estimating BF uses transdimensional MCMC, which concentrates on estimation of the ratio of model posterior. Therefore, we can simply calculate BF which equals to model posterior ratios divided by model prior ratios (see Fig. 3). By the way, does this method seem to be independent of parameter prior?
https://forum.cogsci.nl/uploads/026/YWZONIDQOAOG.pngFig .3
Accordingly, I would like to know the algorithm of BF in JASP. If JASP uses the first method, I understand why the parameter prior affects BF and model parameter does not. Next, I do not understand why the change of model prior does not affect model posterior.
If JASP uses the second method, I do not understand why the change of model prior does not affect BF and parameter prior affects BF.
Please reply to me at your convenience.
Kind regards,
Wang
Both methods estimate the same quantity -- the BF, which depends on the parameter prior but does not depend on the model prior. In your equation for the MCMC method, the change from prior to posterior odds equals the BF, which is the ratio of marginal likelihoods, which is a prior-weighted average likelihood. What JASP uses depends on what is possible (obviously we prefer an analytic solution), what is most convenient, what is available in the packages we call, etc.
Cheers,
E.J.
Hi @EJ ,
I have not understood why BF is unaffected by model prior regarding the equation below. We can obtain model posterior ratios from transdimensional MCMC, then calulating BF through model posterior ratios divided by model prior ratios. Adjusting the model prior in JASP, P(M) changes, so the model prior ratios should also change. Therefore, why does BF not change?
Best wishes,
Wang
Hi @EJ ,
Maybe I have misled you. I found an issue when I used Bayesian ANOVA in JASP. In version 0.16.3, the function of adjusting model prior was added to Bayesian ANOVA. The P(M|data) did not change when I adjusted model prior. Therefore, I was confused by the problem that why P(M|data) or BF did not change given the different model prior (see figures using different model prior and same parameter prior below). At least, should P(M|data) change?
The analysis used example data "stroop" in JASP.
Sincerely,
Wang
I think this is a bug! Well spotted. We'll fix this before the next version.
Looking forward to the new release!