Logistic Regression - Unusually Low Odds Ratio

zaeem_hadi

Hi,

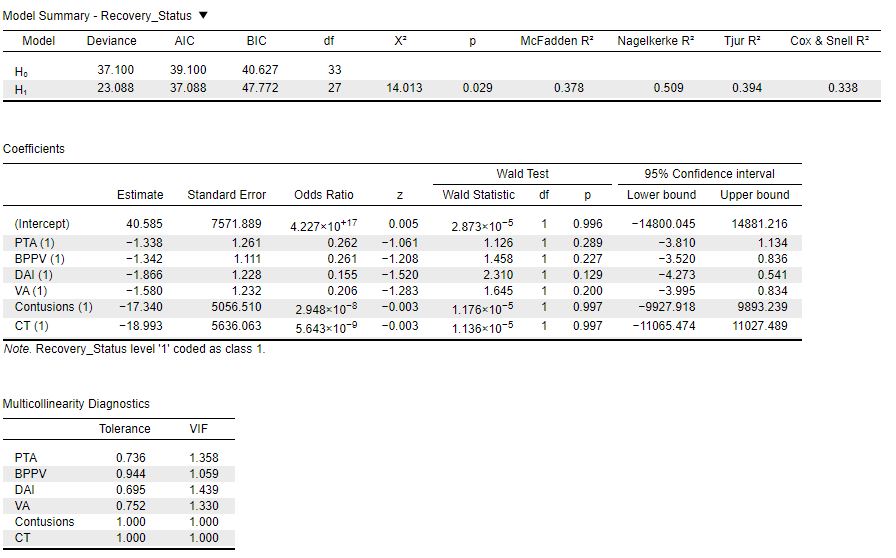
I am performing logistic regression in JASP 0.17.1. I have a sample size of 39 and I am using 5 predictors. There are two predictors in the model who have extremely low Odds ratio. Not only that, when I add these predictors as factors Odds ratio for intercept becomes extremely large (10^17). If these two predictors are removed, the odds ratio of intercept seems okay.

Note that I have tried keeping those two predictors as factors and excluding all others as, however, the odds ratio is still very large for these two.

All the data is in form of 0/1s. I am not sure what could be the reason for this and whether I am doing something wrong. See attached table of results.

It would be great to have an opinion on this.

Thanks.

Zaeem

EJ

1. Using 5 predictors when you have 39 observations is pushing it.
2. Help file: "Odds ratio: Odds ratio is an indicator of the change in odds resulting from a unit change in the predictor." You can see that the standard error in the Confusions and CT estimates is very large, so one unit change won't make much of a difference; hence, the odds ratios are very low (note the minus sign in the exponent).
3. If you look at the estimates and their standard errors, there is no evidence for any effect
4. What I do find remarkable is that the standard error in the intercept is so large, but the odds ratio is very high. I will ask the team about this.

EJ

zaeem_hadi

Thank you.

I have tried using the two predictors of CT and contusions to see if it was due to the number of predictors in the model. However, the standard error is still quite high. I am not sure why these two predictors would have such a high value of standard error, considering that the data is quite similar to other predictors.

Also, if I use the robust standard error, Wald's test indicates that the two predictors with high standard errors are significant, even with such a low odds ratio.

Best,

Zaeem

EJ

I am not sure what is going on here -- could you share the data? (if you don't wish to share publicly, you can email me EJ.Wagenmakers@gmail.com or E.M.Wagenmakers@uva.nl)

zaeem_hadi

I have just looked at the data again to see what is going on, while I wait for clearance to share the data.

I think the reason for these unusually high standard errors is that all the subj's with recovery_status (DV) of 0, have CT and contusion as 1.

So there is not a single case with CT and contusion 1 and recovery_status 1, unlike other predictors.

Essentially that means that having a CT and contusion of 1 perfectly predicts recovery_status of 0 (obviously with limitations of sample size).

But would it be statistically correct to use these predictors in the model, and their accompanied odds ratio, given the uncertain estimates and possible impact on the odds ratio of other predictors?

Thank you for your time.

Zaeem

EJ

This strikes me as problematic

EJ