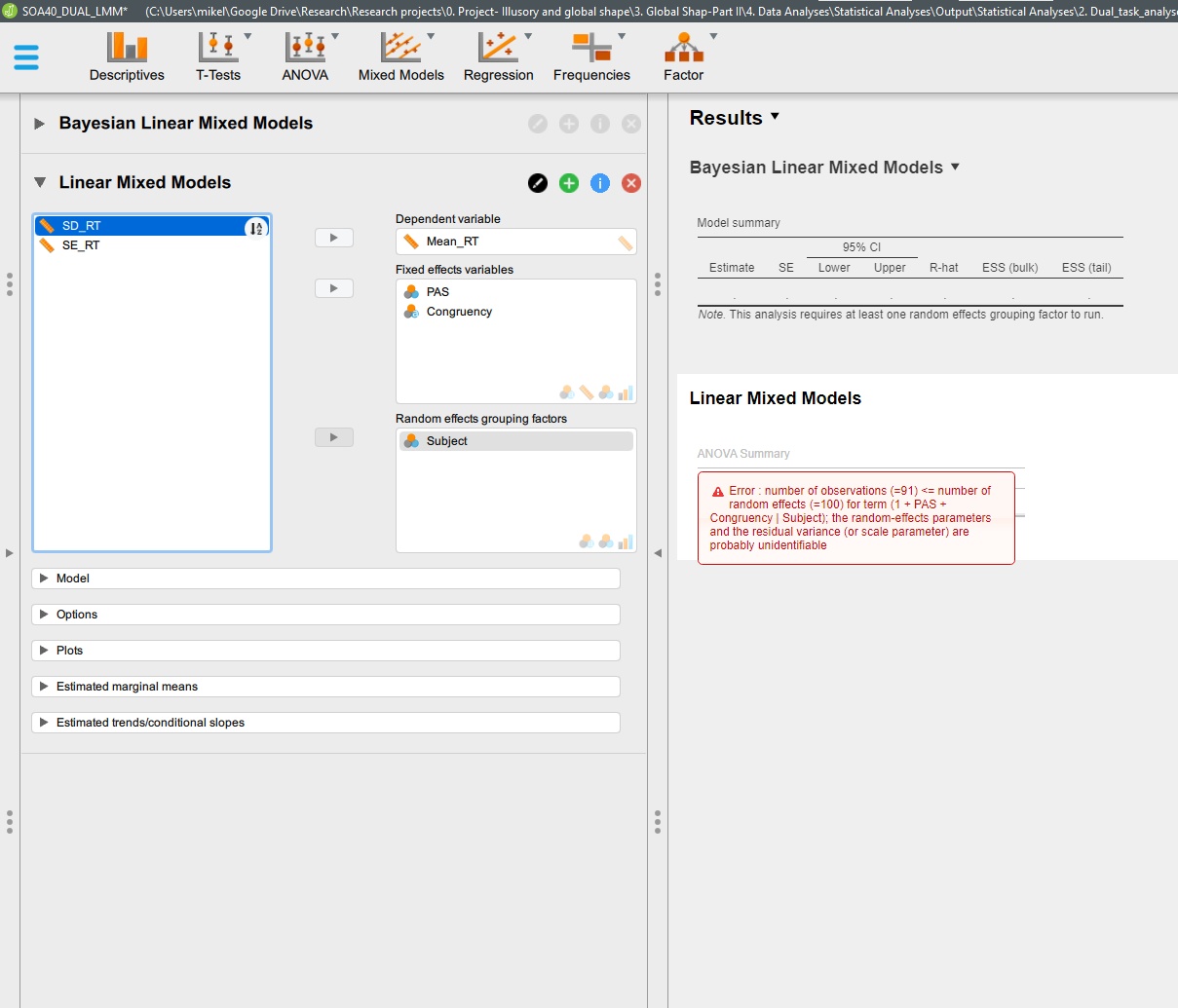
Linear mixed model error : number of observations <= number of random effect

MikJ

Hi,

I'm running a linear mixed effect with id (Subject) as random effect (20 participants), PAS (4 levels) and Congruency (2 levels) as fixed effects. The datasets contains missing values, for example, there might be some participants without rows for PAS3 or PAS4 levels, so the total number of rows that I have in my dataset is 91 (instead of 160 that would be a dataset without missing values).

I'm getting the following error: "Error: number of observations (=91) <= number of random effects (=100) for term (1 + PAS + Congruency | Subject); the random-effects parameter and the residual variance (or scale parameter) are probably unidentifiable.

Any idea how could I circumvent this problem?

Thanks,

Mikel

patc3

Hi Mikel, it's really tough to see where the problem is without seeing what the data look like... What about Congruency, are you sure it's only got 2 different values? I'm bothered by the fact that it's a text variable

Some descriptive statistics might help to diagnose the problem (or a snippet of the data). I suggest you show descriptives/frequencies for all 4 variables involved

MikJ

Hi patc3,

Thanks for your comment. Here how the data looks like

And here some descriptives. Sorry I do not use JASP to do my analyses so I'm not sure how to plot them for both variables

patc3

I've now discovered that the default model in the mixed-models module is way too complex: by default, all possible interaction terms are included as fixed effects (under the Model section in the analysis), and all possible random slopes (including interaction terms) are included as random effects (under the Random effects section in the analysis).

So you have to do two things:

1) under Model, remove from the Fixed effects all the interaction terms (unless you want them)

2) under Random effects section, uncheck all variables except intercept (unless you want random slopes, which you can always add later); if you haven't done step 1 (remove interaction terms from the fixed effects under Model), then you will also find interaction terms here, which is absurd

I think these defaults come from a paper titled "Random effects structure for confirmatory hypothesis testing: Keep it maximal", but they are very unfortunate, and not at all practical.