interpretation of results of Bayesian linear regression

Weijian

Hello guys,

I am performing a Bayesian linear regression analysis with covariates.

My aim is to investigate the relationship between A and B.

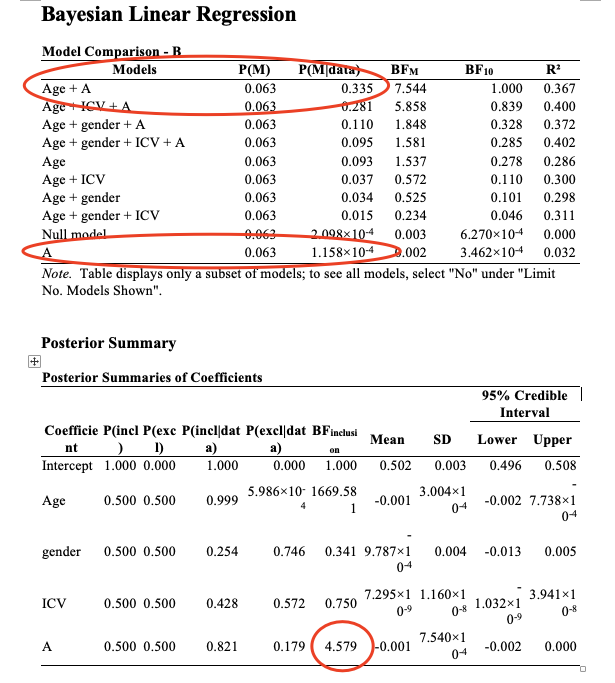
As the following results show, when including A in the model, odd decreased. However, the BF(includ) of A is 4.5.

In this situation, can I draw the conclusion that A is associated with B?

EJ

In the top table, the result from the bottom row means that the model with A alone fairs relatively poorly. However, what matters is the change from prior to posterior probability for all models that include vs exclude A, and this yields an inclusion BF of about 4.5 -- moderate evidence for the association.

EJ

Weijian

Hi EJ,

Thanks for your answer!

Can I describe the result like this:

A showed moderate evidence of being correlated with B (R2 = 0.032, β = -0.001, BFincl = 4.579) ?

Best,

Weijian

EJ

Well, I think there is moderate evidence in favor of including this predictor in the regression equation. The R2 value for the A-only model is not really relevant for this. And the beta coefficient is not only very small, it is negative as well; you might want to check out whether the sign is consistently positive or negative across the different models, and what this would mean.

Cheers,

E.J.

Weijian

Thank you so much, E.J..

Best regards,

Weijian