Different post hoc contrast results of Generalized Linear Mixed Model in R and JASP
Hi every one!
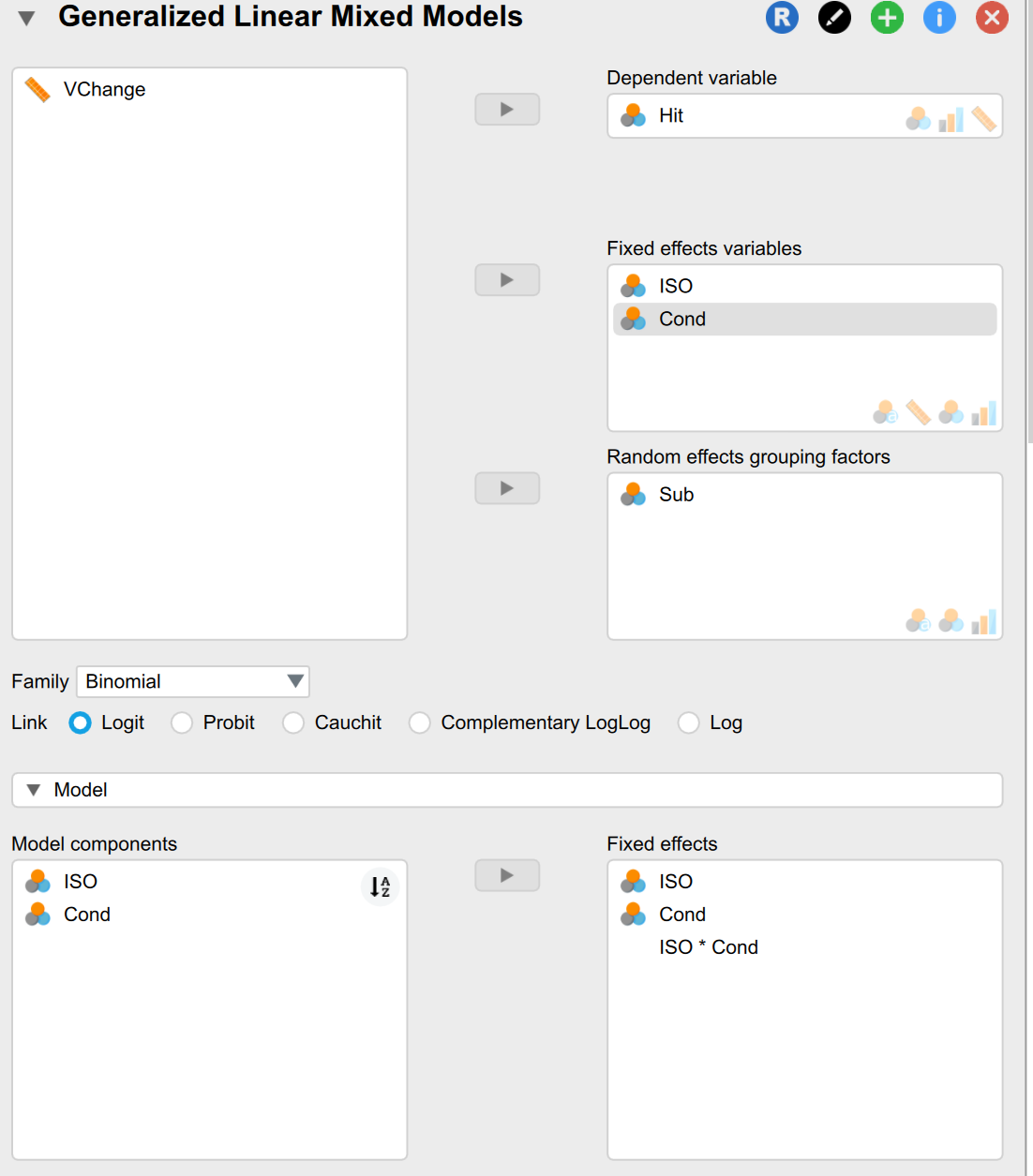
I am trying to fit a GLME in JASP. The dependent variable is 0 and 1 so I chose the family as Binomial and the link funtion as logit. Here below is my settings and results:
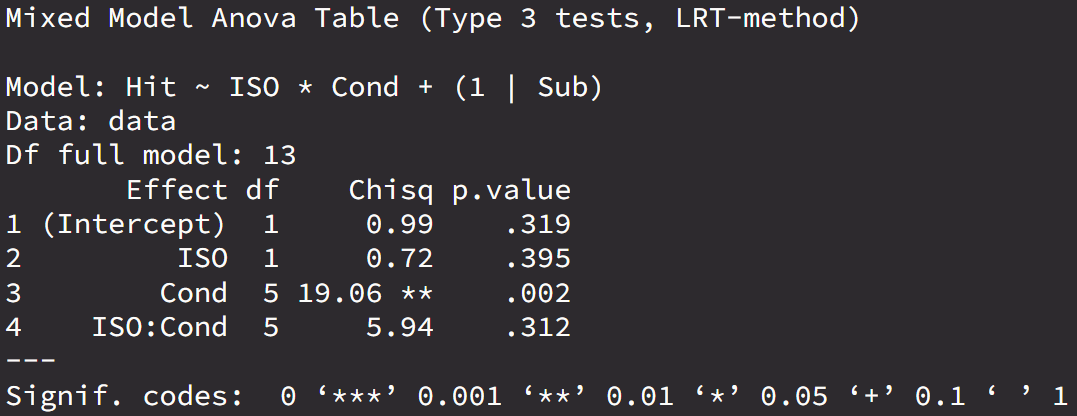
My function is "Hit ~ ISO * Cond + (1 | Sub)":
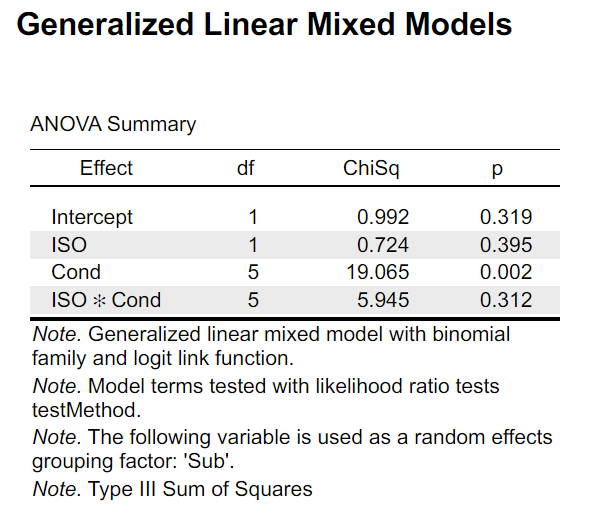
The results:
I tried to replicate the results in R:
fit = afex::mixed('Hit ~ ISO * Cond + (1|Sub)', data = data, family = binomial,
method = 'LRT',
test_intercept = T)
fit
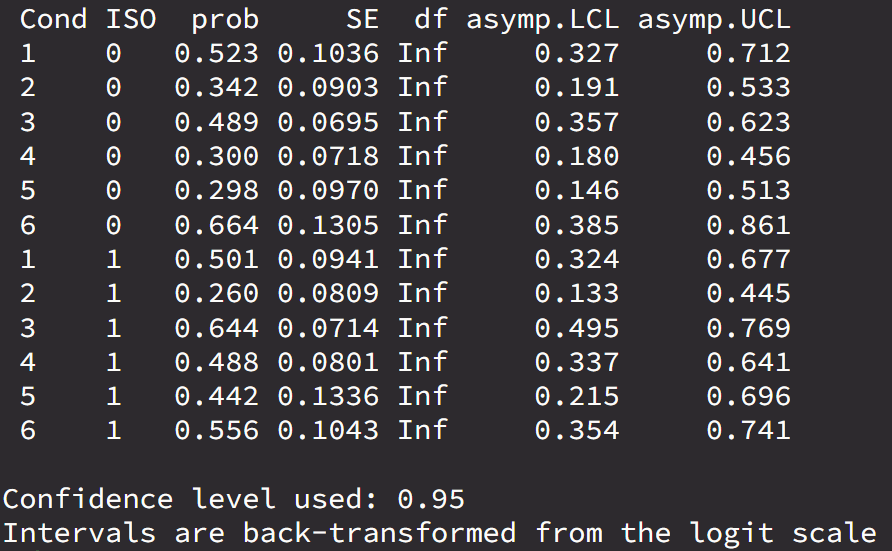
emmeans(fit2, ~ Cond * ISO, type = 'response')
The model fit result is totally the same:
The emmeans were also compeletely the same:
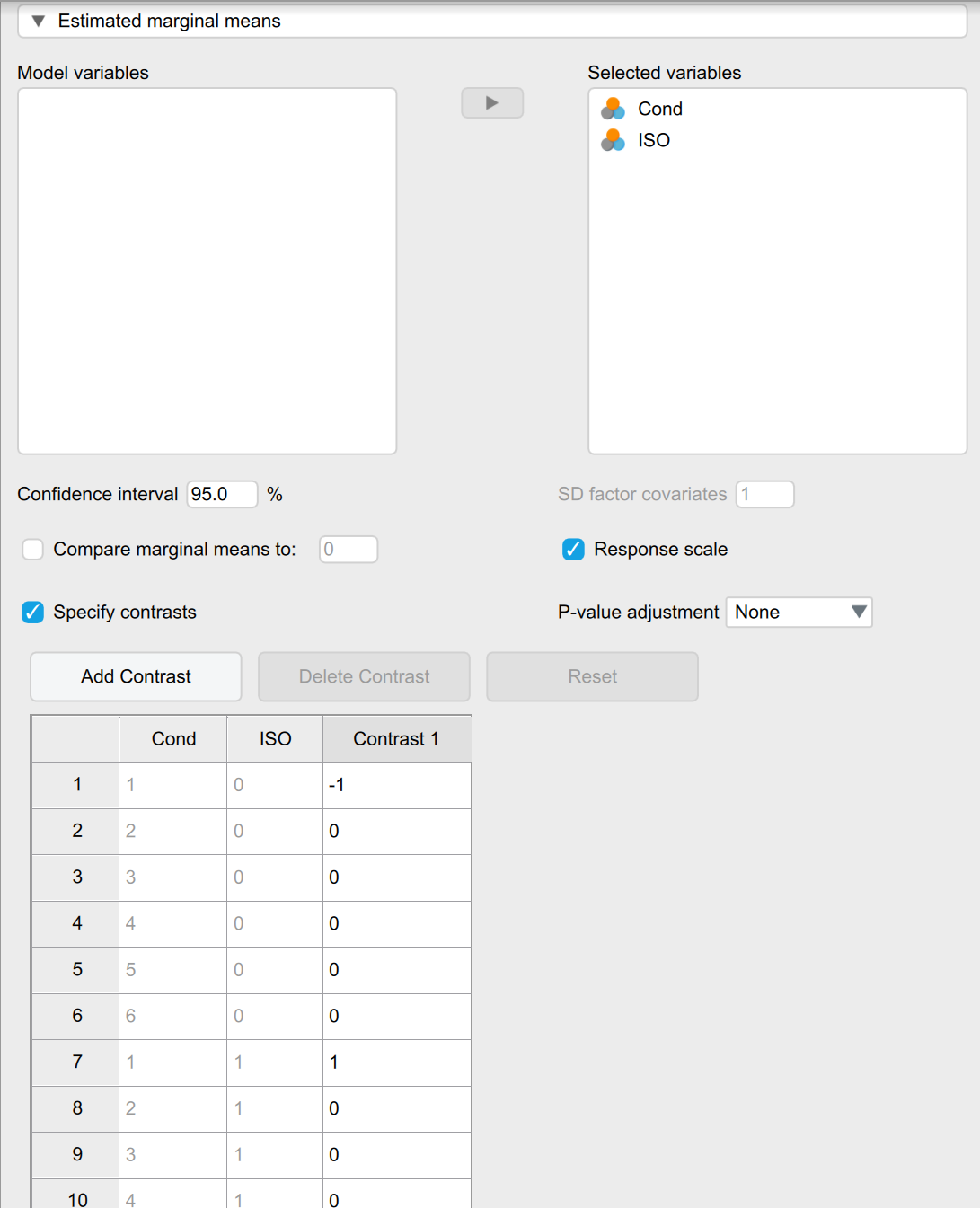
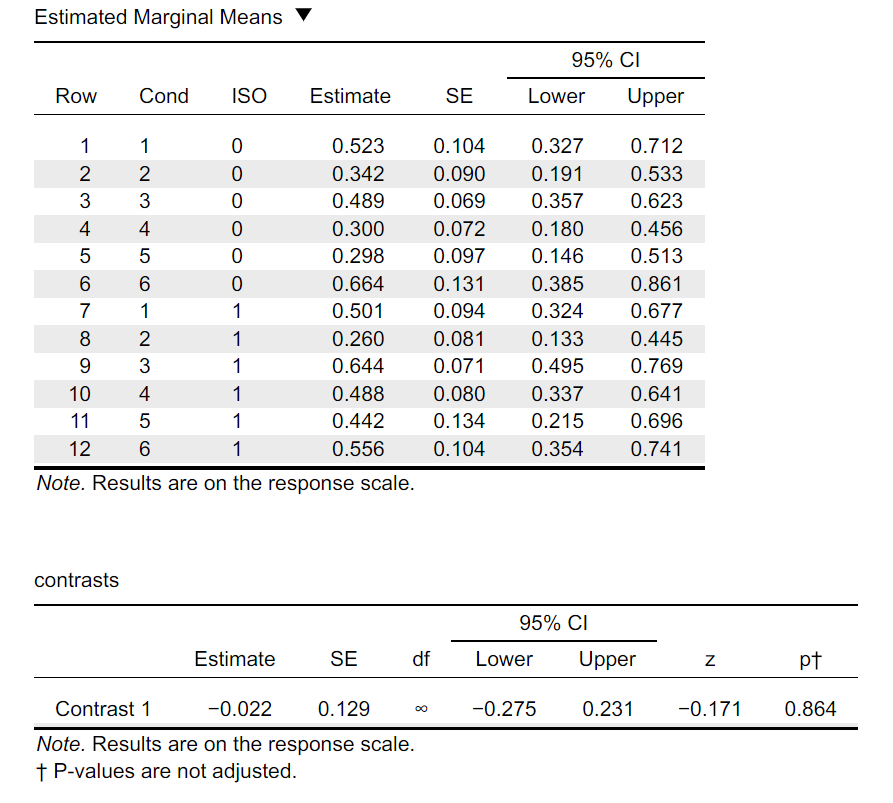
However, when I apply post-hoc contrast, the results are quite different (in JASP, the contrast is Cond1_ISO1 - Cond1_ISO0):
emmeans(fit, revpairwise ~ Cond * ISO, type = 'response', at = list(Cond = '3'))
The emmeans function in R returns estimation of odds.ratio, and the p.value is 0.0806. However, the estimation in JASP is not the same, though I have set all visible parameters identical (I hope so).
As far as I know, the contrast bwteen two levels in model with logit link function should return a odds.ratio other than mean difference. It seems that R returned the desired result. I also tried to reverse the contrast in JASP, and found that the software returned the opposite of the original number rather than the inverse. So I am not sure whether JASP is returnning the right result, or there are additional parameters should be pre-set.
Thanks a lot for your time!😊



Comments
Hi Howard,
Thanks for posting the question. I think that the main difference is that you do not compute the contrast on the outcome scale (probabilities) but rather on the latent model scale and then transform it into odds ratios. I.e., under the specified settings, JASP computes the difference between the estimated probabilities, i.e., (1st and 7th row: probability difference: 0.501 - 0.523 = -0.022) but your R settings computes the difference on the logit scale and transforms into OR, i.e., OR = (0.644/(1-0.644)) / (0.489/(1-0.489)). If you deselect "response scale" in JASP and compare the corresponding levels as in R (i..e., 3rd and 9th row), I think you will obtain the same output.
The question is what inference you are interested in: whether in the differences in the latent scale or on the probability scale, as these might give different results -- this is however theoretical question for you and your goals :)
In case you wanna get the difference in probabilities in R too, the following code snippet should illustrate how:
emm <- emmeans::emmeans(
object = fit, ...,
type = "response"
)
emmeans::contrast(
emmeans::regrid(emm),
contrs
)
Cheers,
Frantisek
Dear Frantisek,
Thanks a lot for your quick response! I think we are going to the right direction.
Sorry I didn't specify the same contrast in two softwares, and I tried the settings again (Cond1_ISO1 - Cond1_ISO0 this time, with factor contrast method set as contr.sum).
JASP (response scale checked):
R (specified type = 'response'):
result:
The pvalues and zvalues are the same, but R still calculated the odds ratio ((0.501/1-0.501)/(0.523/1-0.523)) even though the emmeans returned with probs, and JASP calculated the difference of probs (0.501 - 0.523).
I reviewed relative concepts and re-tested the codes, and get the following conclusion:
In both JASP and R, the 'response scale' both means probability, which is y = logit-1(ax + b),
and for non response scale, the emmeans was calculated in logit scale, which is In(y/1-y) = ax + b
In JASP, regardless of whether 'response scale' is checked, the contrast is simply the mathematical difference between the two levels.
In R, things are somewhat more complicated.
When defining type = 'response', and ratio = T (by default), the emmeans are probs, but the contrast is the odds ratio ((PA)/(1-PA)/(PB)/(1-PB)). While if defining ratio = F, the emmeans are still probs, but the contrast is the mathmatical difference between logit values (Ln(OR)).
When not defining type = 'response', the emmeans are logit values, and the contrast will always be difference between logit values (Ln(OR)), no matter how ratio parameter is set.
I hope I correctly understand this, and I think it's just the different in the logic of designing between two softwares.
Thanks again for your response and hope this post can help others.😉
Just to check, did you use the 'emmeans::emmeans' function to create the marginal means object and then the 'emmeans::contrast' function to compute the contrasts? We did explicitly separate the calculations in the underlying implementation to always keep the corresponding scales (it seems like that using only the 'emmeans::emmeans' function does not enforce the same scale for the automatically calculated contrasts?)
Cheers,
Frantisek
Hi Frantisek,
In the example above, I did conduct the contrasts using a single call of the emmeans function. I tried to separate these two steps by combining emmeans() and contrast(), and the result was the same as that obtained with just emmeans() in R.
😳
Howard
Hi Howards,
Hmm, that's quite interesting that R produces the output on OR scale (I would expect it to use the specified contrasts by emmeans directly).
Also, in JASP we use a combination of the two functions too, i.e.,
Do you see any other immediate difference from your implementation?
Frantisek
Hi Frantisek,
For now, I only found this difference in GLME module. I think this vignette that may provide some clues:
In the last part, the paragraph mentioned that “when
contrast()(orpairs()) notices that the response is on the log scale, it back-transforms contrasts to ratios when results are to be ofresponsetype”, I think it's also applied in logit transform.I'm not sure if it's a matter of version. The version of my currently using
emmeanspackage is1.8.9. Unfortunately, I didn't find changelog of all versions ofemmeans. But I hope this helpful.Howard
Hi Howard,
Thanks for catching that out--I haven't used emmeans for quite a bit and didn't know about this. I finally had a bit more time to take a deeper look. Using the following code, it seems like that using
regrid(as we do in JASP) helps with side-stepping the automatic back-transformation. When designing the JASP output, we wanted to have consistent output (i.e., both marginal means and contrasts are on the same side scale) so that's why we did that--but I wasn't aware about the default behavior. You can reproduce the difference with the code bellow:library(afex) library(dplyr) library(emmeans) data("stroop") stroop_e1 <- stroop %>% filter(!is.na(acc)) %>% filter(study == "1") %>% droplevels() fit <- mixed( acc ~ congruency*condition + (1|pno), data = stroop_e1, method = "LRT", family = binomial ) emm <- emmeans(object = fit, "congruency", type = "response") contrast(regrid(emm), list(c(-1, 1))) contrast(emm, list(c(-1, 1)))Cheers,
Frantisek
Hi Frantisek,
Thanks for following! I reviewed the code in your link and I think we have found the reason.
I am thinking whether it is convinent or under your consideration to add an option or some other ways in JASP to return the result of OR. Because for model with logit transform, the contrast may be more interpretable with OR.
Thanks again for your time!
Howard
Hi Howard,
Yes, I can see that as a useful feature indeed (so far, you can obtain the OR by exponentiating the non-response scale output manually--in case someone else comes to this thread later).
Thanks for looking into this with me,
Frantisek
cheers!🍻