Combining BFs for distinct hypotheses
I am looking for a principled way to combine Bayes Factors across experimental conditions. My first thought was to treat it as a meta-analysis, but then realized that this is problematic, because our hypothesis differs across conditions. In short:
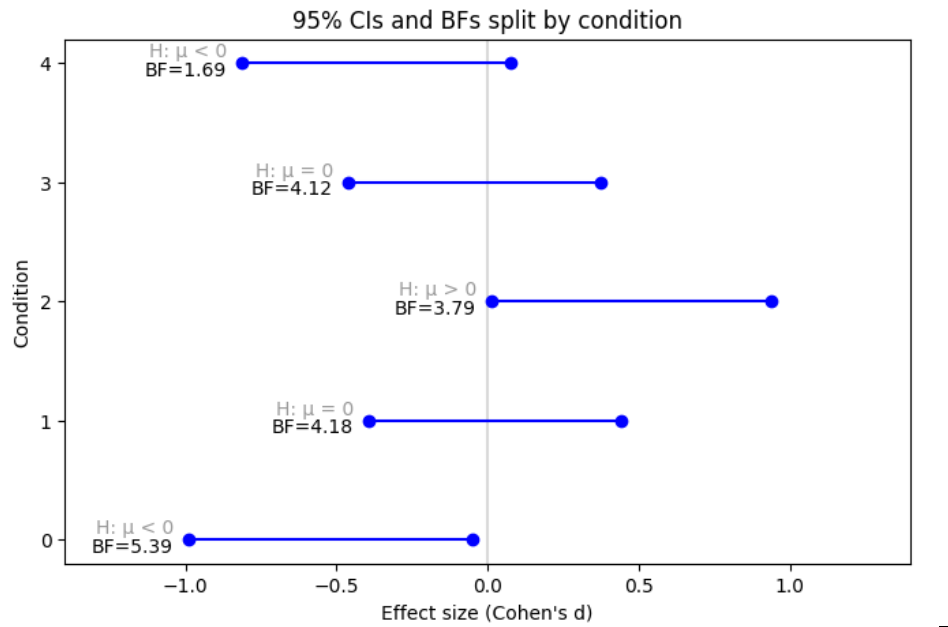
- we have data from 20 subjects who each performed trials in 5 conditions (C0, C1, C2, C3, C4)
- what goes into the analysis is a trial-averaged measurement of the dependent variable (DV) for each condition (hence, the data consist of a 20 x 5 matrix)
- we have a theory that makes a specific prediction for the DV in each condition: negative in C0 and C4, positive in C2, and zero in C1, C3
- using Bayesian t-tests, we find in each condition that the data support the hypothesis for that condition:
(For clarity: the BFs in conditions 0 and 4 were obtained as BF10 in a t-test with "< 0" as alternative hypothesis, the BFs in condition 2 was obtained as BF10 in a t-test with "> 0" as alternative hypothesis and the BFs in conditions 1 and 3 were obtained as BF01 in a t-test with "≠ 0" as alternative hypothesis.)
The evidence in each individual condition is anecdotal to moderate, but it feels like the combined evidence should be stronger (after all, consistently throughout the conditions, the evidence points in the hypothesized direction).
My question is if anyone can point me to a resource that explains how to combine these 5 BFs in a principled manner. One thought for combining C0, C2, and C4 I had, is to flip the sign of all data in C2 and then treat those three conditions as different studies in a meta-analysis (it's reasonable to assumed that the effect sizes are the same in those three condition, but just with different sign in C2). But the same trick cannot be used to also get C1 and C3 into the mix (because there the hypothesis is the absence of an effect).
Thanks in advance for any pointers on this!


Comments
I think that you might try a procedure such as Bain (also a JASP module); in general, the work of Herbert Hoijtink, Irene Klugkist, Joris Mulder et al. has focused on these sorts of constraints across conditions.
EJ