Network analysis -- Bootstrapping

MBD

Hi everyone,

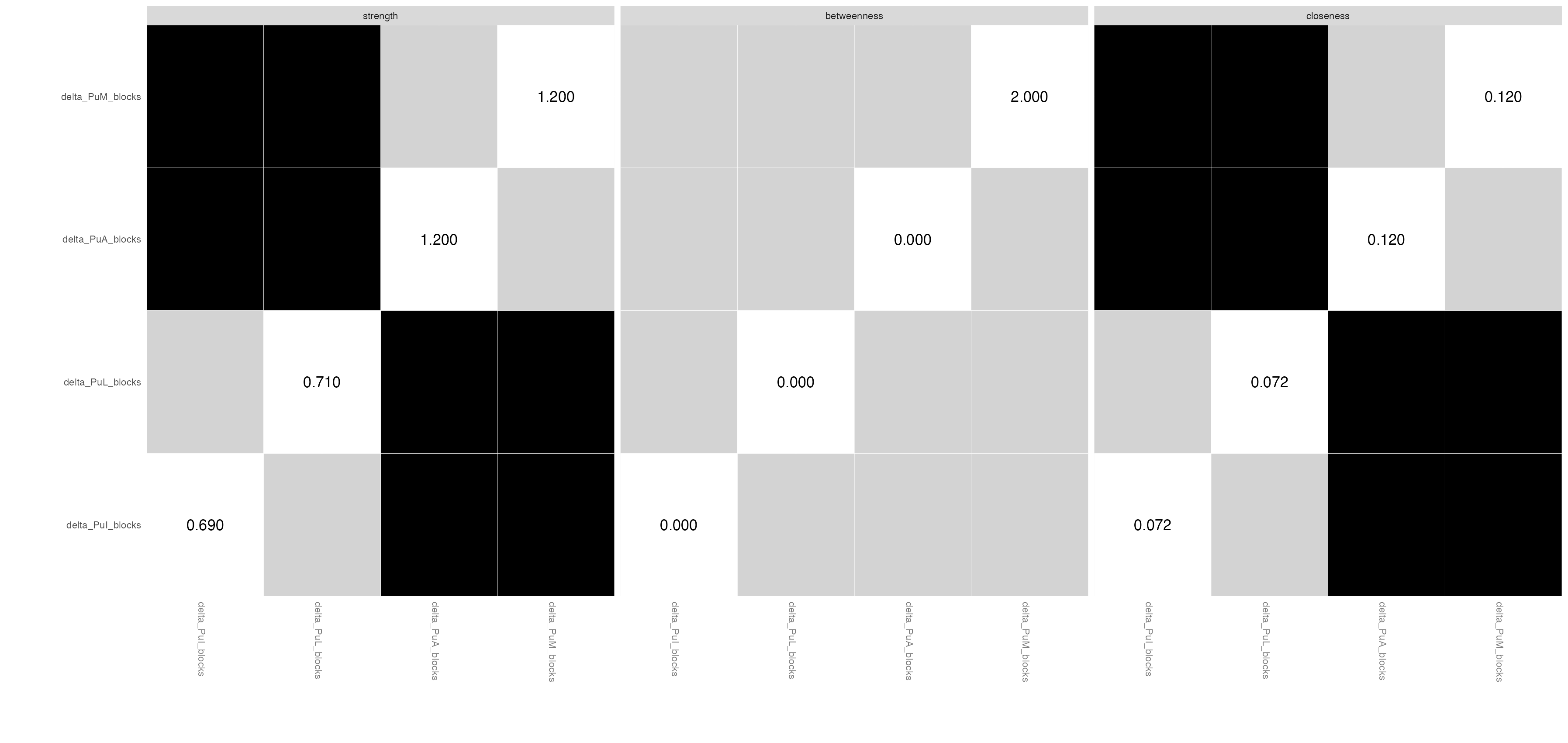
I'm trying to understand the black-gray-white output I got when bootstrapping the centrality measures of network analysis. I'm aware of two tutorials recommended in this forum but still, I don't understand how to interpret my results. The output shows a matrix of each node with all other nodes. Black color indicates significant difference while gray indicates nonsignificant results. But what that means?

Let's say there are two nodes A and B. Does the output represent this process:

1) Deference between the observed A and observed B.

2) Deference between the bootstrapped A and bootstrapped B.

3) Creating a distribution of 2.

4) Comparing the place of 1 on the distribution of 3 and decide if it's significant or not.

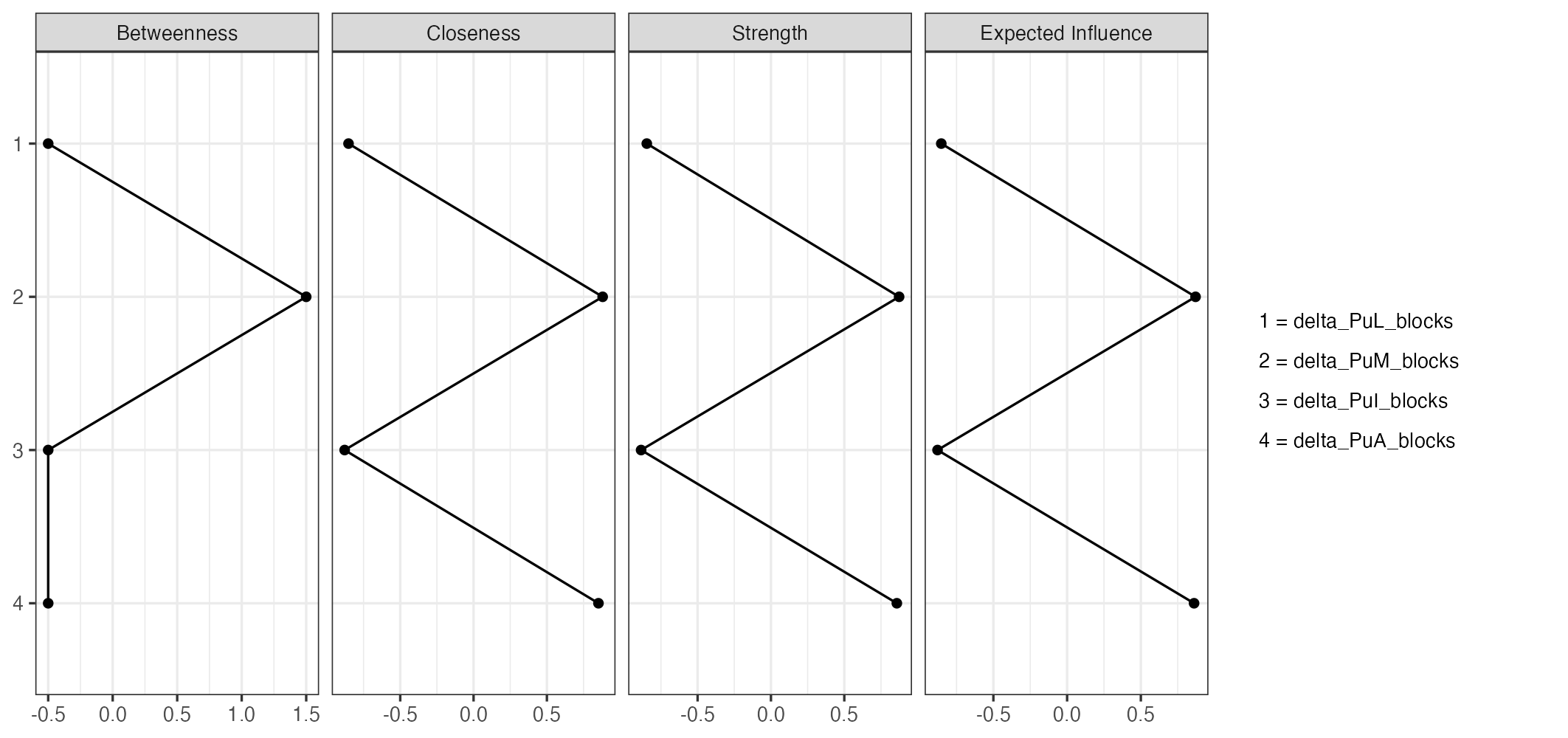
If this is the case, that means, black squares are unstable and gray squares are stables? -- but this doesn't make sense to my results. Please see the attached Table 1 shows that nodes 2 and 4 have stronger centrality measures in the network. However, the bootstrapping shows that the difference between node 4 and: 1 & 2 is not stable. This doesn't make sense to me. I think my interpretation of the results is not correct.

Please let me know what you think and how to understand these outputs.

Thank you so much,

Muhammad Badarnee

EJ

I've asked the team

Cheers,

E.J.

vandenman

Hi,

What happens is that

1. The data are bootstrapped
2. A network analysis is conducted on each bootstrapped sample
3. For each bootstrapped analysis, the difference between the edges weights (or centrality measures) is computed.
4. Those form a distribution, and a confidence interval can be computed.
5. If 0 does not lie in the confidence interval, then there is a significant difference and the square is colored black, otherwise, it is colored grey.

Note that in the two screenshots, the order of the nodes is not the same. In the centrality plot, it's

1. PuL
2. PuM
3. Pul
4. PuA

whereas in the bootstrapped plot it is

1. PuM
2. PuA
3. PuL
4. Pul

If I look at the centrality plot (either closeness or strength) then it looks like nodes 1 & 3 differ from 2 and 4. This is corroborated by the bootstrap result. It appears as if there is also a difference in betweenness among the nodes (e.g., node 2 vs the rest), but the bootstrap confidence interval does include zero, so this difference is not significant.

Hope that helps,

Don

MBD

Thank you EJ and Don for clarifying this point. I wonder if there is an option to extract the actual values of the 95% CIs of the bootstrapped distribution of the differences between each pair of nodes.

Thank you,

Muhammad.