JASP Bayesian rmANOVA: Order of factors influences output
Hi,
I am running a Bayesian rmANOVA in Jasp 0.18.3 with 3 repeated measures factors (Session, Position, Distance) and 1 between subject factor (Group). I noticed that depending on the way my datasheet is organized, I get different outputs (leading to different conclusions regarding the interaction effects I am interested in).
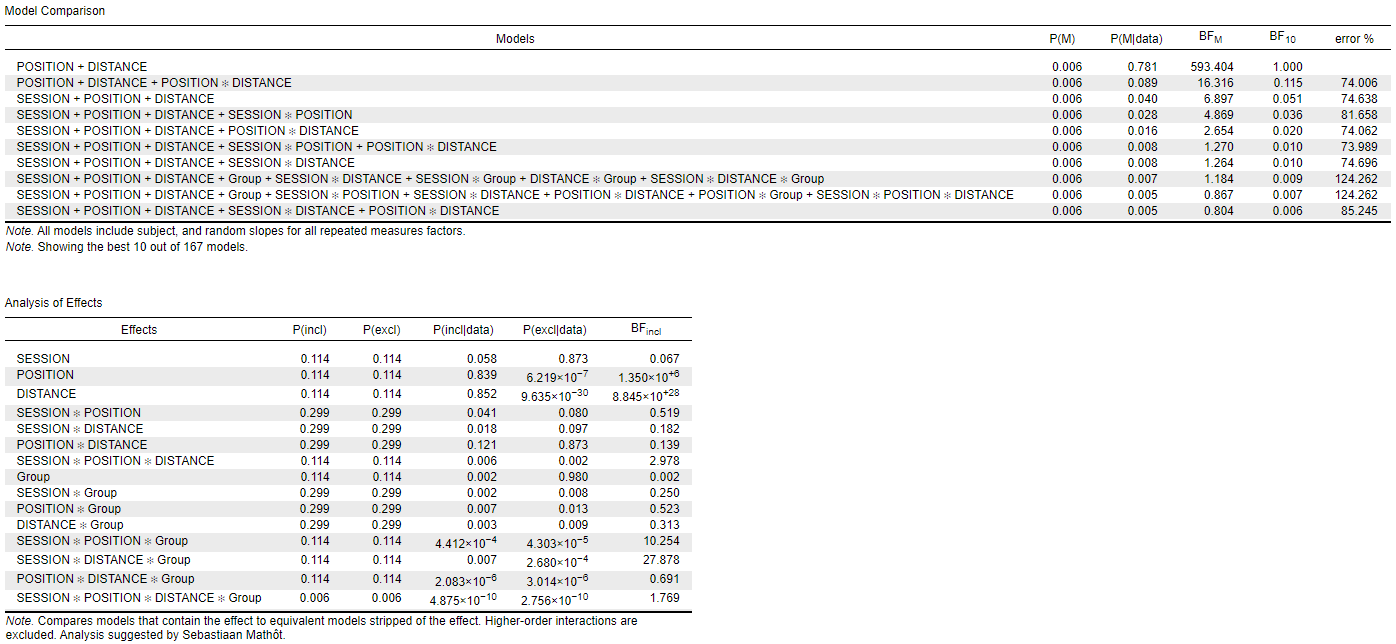
When I put the factors in the order "Session, Position, Distance" (order 1), I get the following results:
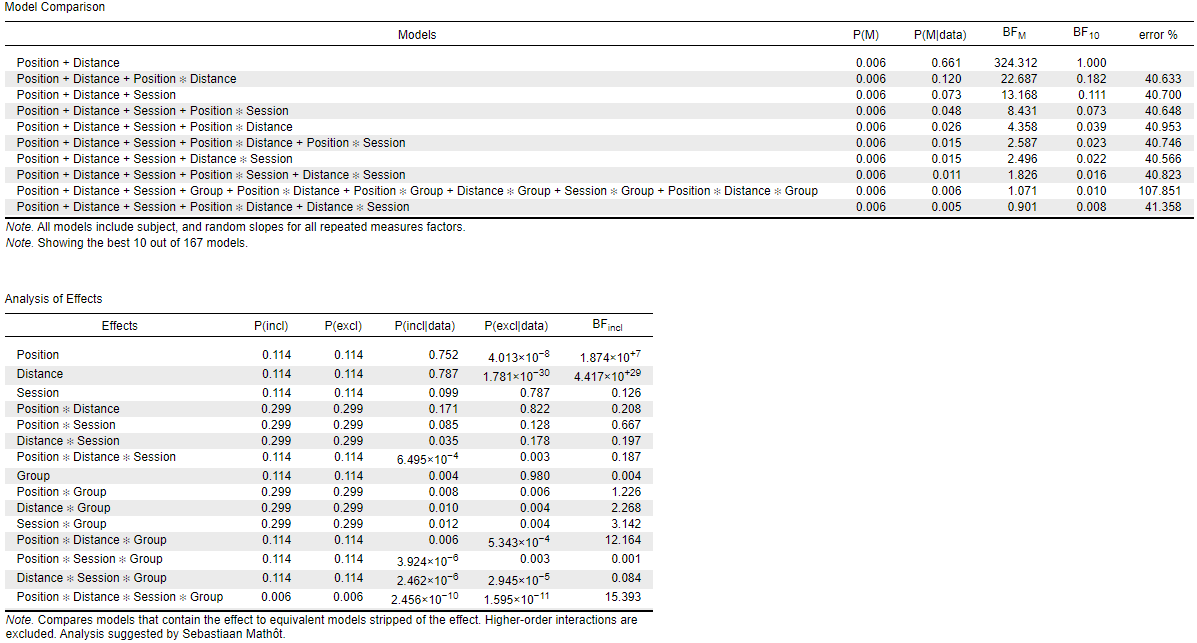
while when I put the factors in the order "Position, Distance, Session" (order 2), I get the following results:
I noticed also, that depending on the order of factors in the datasheet, the model terms in the model section are ordered in a different way. I guess that is the reason why I get these diverging results.
The interaction I am mainly interested in is the Group*Session: its BFincl is either 0.250 (order 1) or 3.142 (order 2). I am also interested in the Distance*Session*Group: BFincl of either 27.878 (order 1) or 0.084 (order 2). --> completely different interpretations.
My concern is that I don't have a better reason to choose order 1 than order 2 or vice versa. How to order the factors in an objective correct manner to get the correct results? Is there a rule?
I would be very grateful for any hint of an answer!
Thanks.


Comments
I'd like to offer a possibility, which may be tested quickly for you.
I don't know if you have set this before, but you can try to first set the same seed for both runs before comparing these results to ensure the repeatability, which shoule be set in the additional options.
I also run my data to test what you propose. I acquire the following approximately identical results.
and
But still, I am also curious about why there is still slight difference between these two runs, even when the seeds are set the same.
Hi Chen,
Thank you so much for your answer!
I tested what you suggested (setting up the same seed : I put 1), but unfortunately, it didn't attenuate the difference between the 2 results : now it gives the following BFincl: Group*Session: 0.051 (order 1) or 4.298 (order 2), and Distance*Session*Group: 43.006 (order 1) or 0.093 (order 2). --> So I don't think that was the problem.
Also, I think that in your results the difference between the orders is only slight because you have only 2 factors (compared to my data with 3 within and 1 between factors).
Thank you again for your time!
UPDATE: I checked if the unconsistency of the outputs depending on factors orders was linked to the new versions of JASP (from 0.16.3) which include now random slopes for repeated measures factors. Indeed, when I use the previous versions (or check the "Legacy results" in the Additional options), there is much better consistency between the 2 orders, and the differences are quite small.
Here is what I get for the 1st order:
And for the 2nd:
Noteworthily, I tried also with JAMOVI which doesn't include the random slopes (to my knowledge), and I get quite the same results as the Legacy results of JASP (consistency across orders of factors).
Now if I understood properly (from the paper: https://osf.io/preprints/psyarxiv/fb8zn), including random slopes is necessary in most designs. So I would still need to use the new versions of JASP, but I don't know how to decide the "correct" order.
Any help or insight regarding this matter would be very helpful ! :)
This is just a side comment: If I were reviewing a paper, and if the main effects and interaction results depended on the ordering of the entered terms, I'd be uncomfortable with that. I'd also want to see an analysis (e.g., a regular old rmANOVA) in which the ordering did not matter.
R
@andersony3k Thank you for your comment. I totally agree! That's why I am so concerned about solving this issue.. Of course, I also plan to include the regular rmANOVA in the paper: the p value for the interaction is 0.07. That's why I was hoping the Bayesian rmANOVA would give me more information (showing if there is evidence against an effect or if it is inconclusive).
The results cannot depend on the ordering (or at least I don't see how). They will depend on the seed though. I have asked a team member to look at this.
E.J.
Hi MaliAS,
Have you tried increasing the numerical accuracy, or switching to the Laplace approximation?
The error % in your results is rather large and differs between the two runs. This could very well explain the difference in the results between the consecutive runs.
Best,
Don
@EJ thank you for your comment. I tried also to put the seed at 1 for all the runs (in these data and some other ones too), but I still get very different results, so it does not solve the issue.
Hi @vandenman,
I did not try these. I will do both and give you an update.
Thank you!
Best,
MaliAS
@vandenman The Laplace approximation was very fast to run, but it says that some BF could not be calculated, so I can not get the BFincl for the effects I am interested in. But still I notice that all the values that I get in the tables are exactly the same, they did not change with the order of factors.
Order 1:
Order 2:
Otherwise, I tried running the two files with a higher numerical accuracy (100000 instead of the default 10000), and it is way slower (originally, the run lasts a whole day, but now it seems even slower). I will post the results when the runs will be done.
WARNING: in my original message, I realized that there was a mistake in the first screenshot I provided (order 1): it was for another run (with a few different values in the datasheet), so here is the correct one:
And order 2 is still the same:
The BFincl are more similar, but still different (with opposite conclusions for some effects, eg. the quadruple interaction). And also, I have the same issue with other datasets, the two orders give BFincl values that are too different.
Just wanted to correct this mistake. The rest of the values and screenshots are all correct.
So sorry for that!!
I see that your error percentages are very large, around 40%. This means that different runs can give different results. If you set a seed then you should get the same outcome, but this no longer holds when you change the order. So: if you don't set a seed and simply rerun the analysis (but with the same order) do you also find such varying results? I suspect you do, and this would imply that the culprit is in the numerical imprecision of the current MCMC sampling routine. You can remedy this by upping the number of iterations (at the cost of the procedure taking more time) and you can also try the Laplace approximation.
EJ
@EJ Exactly, I tried to rerun the analysis with the same order, and I find varying results too:
Run 1:
Run 2:
As said in a previous message, the Laplace approximation didn't work because it was not able to compute some BFs. And the run with higher numerical accuracy (100000) is still running and I hope to get the results today or tomorrow.
Thank you so much for your help! I will keep you updated as soon as I get the results.
Update: Here is what I get when increasing the numerical accuracy to 100000 (with same seed):
Order 1:
Order 2:
I still get large error percentages, and the BFincl values still vary. At least for most of the effects, the conclusion is the same, but for some (e.g. the quadruple interaction, Position*Distance*Group), the conclusions are very different.
In the end I am not sure increasing numerical accuracy is the solution to the problem.
Any other suggestion? (I put the 2 files on the following link if needed: https://we.tl/t-3EWh2lXMMx)
The error percentages are lower, right?
Another thing you might try is add the components to the null model when you are sure that they should be included. JASP will then take that model as its point of departure, and this means that way fewer models need to be computed and compared.
Thank you for your reply.
The error percentages are lower for some models but higher for some others.
I am not sure I understand what you mean by that. According to me, all my 4 factors have to be tested, none of them is "guaranteed" to be included (I have no a priori reason to include either of them), so I don't think I should include some of them to the null model.
Or maybe I misunderstood your suggestion.
Well the tables suggest that "position" and "distance" need to be included no matter what. This would not allow these to be tested, but it would narrow down the model space -- which could be what causes the numeric instability. So one idea is to focus on a very specific comparison and see whether the results are stable for that one.