Ordinal logistic regression - interpretation of output from JASP
Hello
I am having a bit of difficulty interpreting output from an ordinal regression analysis in JASP. I hope someone in here can help me understand what is going on.
The dataset is from a survey investigating patient experience in the transition between a pediatric (children) epilepsy clinic and an adult epilepsy clinic. The survey consisted of about 25 items, one of these was the overall experience with the transition process.
I am interested in determining whether the answers to some of the other questions can predict the overall experience. As such, my dependent variable is overall experience, which is measured on an ordinal scale ranging from 1-5 (very bad; bad; neutral; good; very good).
I have selected four other items that i believe may in part predict the overall experience:
- Seizure frequency at transition (ordinal: 1-5 with 1 being lower frequency)
- Relative locations of clinics (binary: same location or different locations)
- Accessibility of liaison medical persons (ordinal: 1=always, 2=sometimes, 3=never)
- Other medical conditions (binary: yes or no)
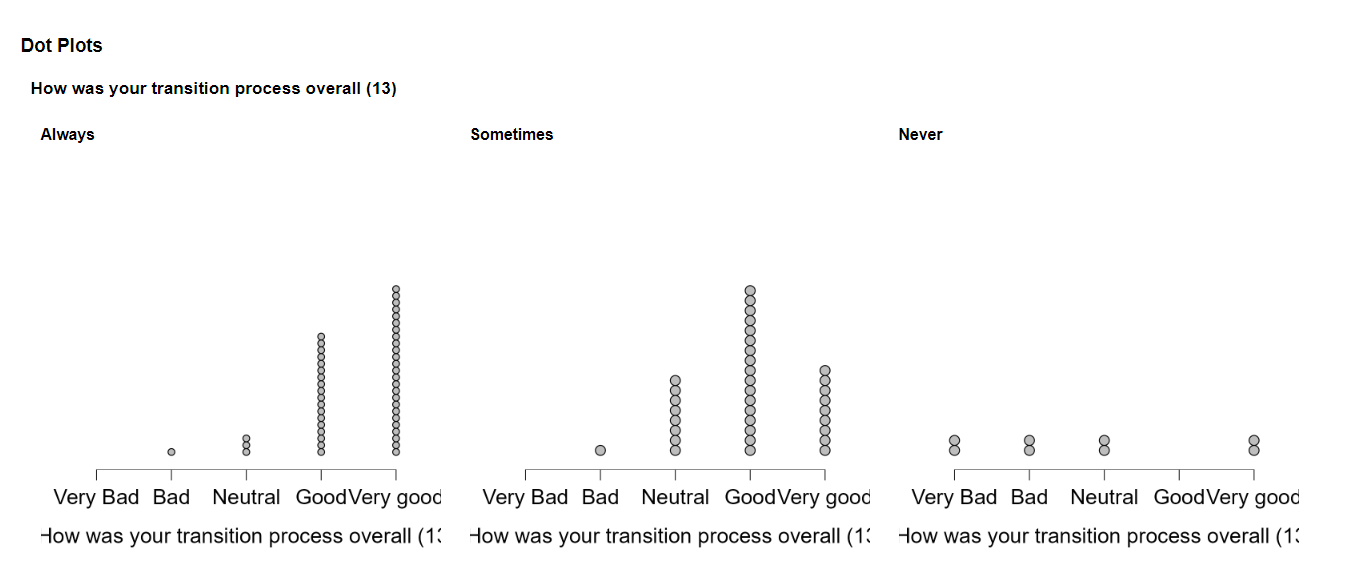
Using accessibility as an example, descriptive statistics indicates that always having access to liaison persons increase the probability of having af better experience:
Please ignore the obvious bias in completion of the survey.
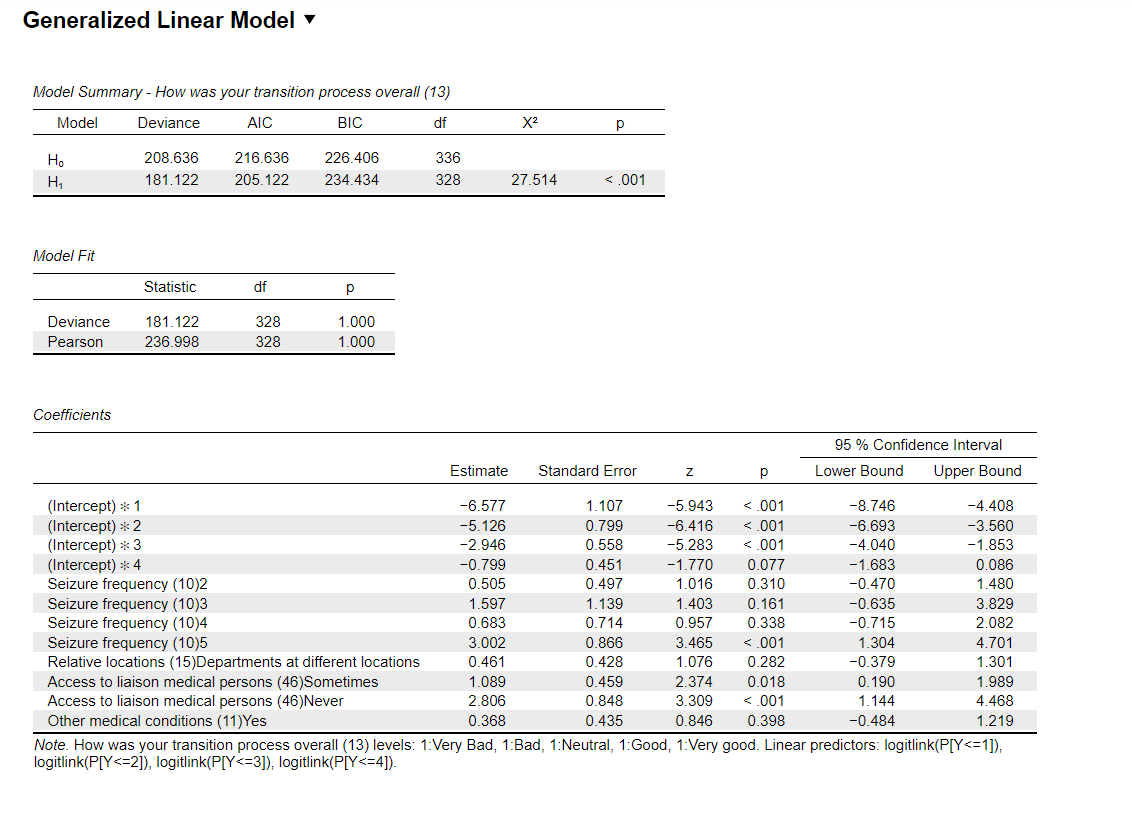
The output from my ordinal regression model looks like this:
From this output, I would interpret that being in access groups "sometimes" or "never" has a higher probability of having a better experience. Which is the oppposite of what the descriptives indicated.
Am I misinterpreting due to my reference group being the group with the best experience? Or am I missing something else?
Hope some can clarify this for me.