how to interpret and report the results of a Baysian repeated measures ANOVA

OR_25

Hello everyone!

I'm not very familiar with Bayesian statistics, so please bear with me. A reviewer has asked me to confirm a non-significant result with Bayesian statistics. I would now like to report the results of a Bayesian repeated measures ANOVA in a few sentences, in addition to my frequentist ANOVA.

However, I am very unsure which aspects of the output I have to mention, and whether it makes more sense to use the BF01 or BF10.

I have tried this so far:

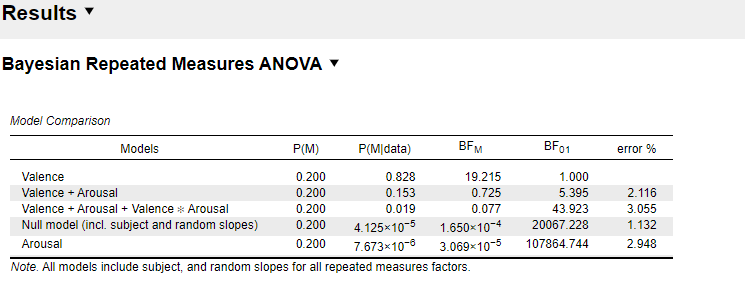
"To confirm our null-result for arousal, we conducted additionally a Bayesian repeated measures ANOVA using JASP (JASP Team, 2019). The Bayes factor (BF01) shows that the data are 5.4 times more likely under the valence-only model than under the model that includes also arousal, and 43.9 times more likely than under the model that includes both main effects and the interaction."

Does it make sense? Is there any information that absolutely must be provided when reporting the results of a Bayesian ANOVA?

I am also very confused about the interpretation of the Bayes Factor. According to The JASP guidelines for conducting and reporting a Bayesian analysis, “Bayes factors between 1 and 3 are considered to be weak, Bayes factors between 3 and 10 are considered moderate, and Bayes factors greater than 10 are considered strong evidence.”

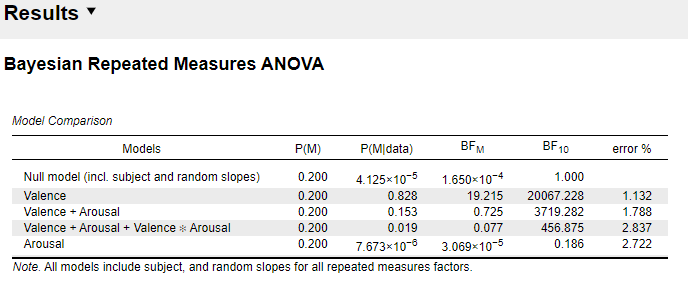
In my case, however, the Bayes factor of the best model is 1. I guess this is because of the setting "compare to best model"? But if I choose "compare to null model", BF10 of the best model gets absurdly high (BF10 = 20067). What does this mean? And which one should I report?

I am very thankful for any help!

EJ

1. Yes that makes sense
2. You are right to select "compare to best model", because this yields the easiest interpretation. All models are then compared to the best one, which is "Valence". The reason for the 1.000 is because the Valence model is compared against itself (so you can ignore this result). If you compare against the null, then all BFs involve comparisons to H0; because H0 does not provide a good account of the data, all BFs will be very large, and this harms the interpretation of the results.

EJ