Bayesian linear regression vs. ancova: understanding the difference in default priors

mservant

Hello,

I'd like to predict scores from variable LARS_TOT using variables UPPS-P_TOT, Age_annees, and genre as predictors. Variable genre is the only categorical variable.

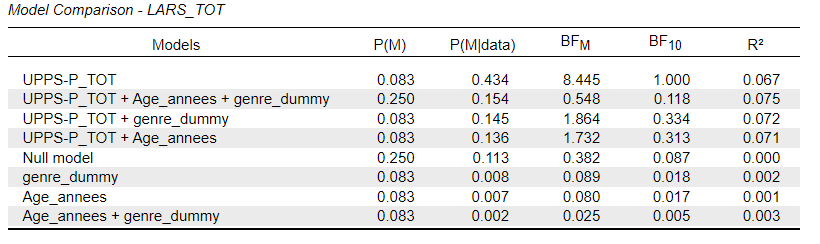
I first computed a Bayesian linear regression (using dummy coding for variable genre), which gave the following table:

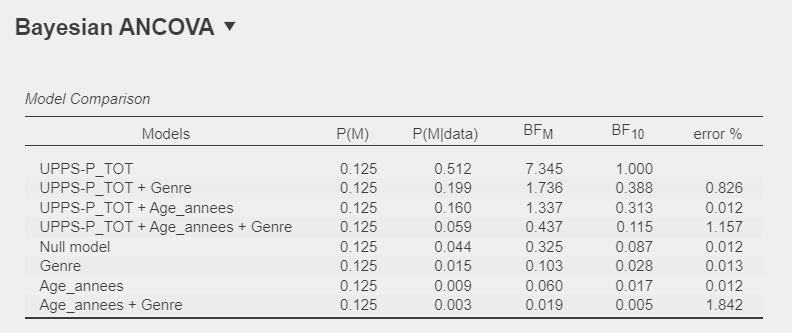
I then computed a Bayesian ANCOVA, using a similar model structure:

I don't understand why the priors are identical across models in the ANCOVA, but not in the linear regression. I’d appreciate any insight you could offer on this.

Cheers,

Mat

EJ

Hi Mat,

The unequal model priors are based on the beta-binomial setup. It can be conceptualized as follows: first, equal prior probability is assigned to each model class (i.e., the class of models with no predictors, the class of models with one predictor, the class of models with two predictors, etc.); next, the probability for each class is divided evenly across the members of that class. This is done to counteract the bias in the uniform assigment that favors models with about half of the predictors in them.

References include Scott & Berger (2006,2010):

@ARTICLE{ScottBerger2006,

 AUTHOR =    {Scott, J. G. and Berger, J. O.},

 TITLE =    {An Exploration of Aspects of {B}ayesian Multiple Testing},

 JOURNAL =   {Journal of Statistical Planning and Inference},

 YEAR =     {2006},

 volume =    {136},

 pages =    {2144--2162},

}

@ARTICLE{ScottBerger2010,

 AUTHOR =    {Scott, J. G. and Berger, J. O.},

 TITLE =    {{B}ayes and Empirical--{B}ayes Multiplicity Adjustment in the Variable--Selection Problem},

 JOURNAL =   {Annals of Statistics},

 YEAR =     {2010},

 volume =    {38},

 pages =    {2587--2619},

}

We are still having a discussion on what method to provide as a default.