repeated bayesian ANOVA

Comments

• sebastiaan

  April 2017 edited April 2017

  Hi VB,

  Regarding your first question, and if I understand it correctly, you're looking for the inclusion Bayes Factor for the valence × group interaction. JASP actually already calculates this for you if you tick the Effects box under output. This is based on averaging across all models with and without this interaction. My understanding is that this comes closest to the F value that you're used to from traditional repeated measures.

  See also:

  • https://static.jasp-stats.org/about-bayesian-anova.html

  Still, even though I have no intention to change them, I`d appreciate some explanations on what these values are for.

  Only the gods know that. And possibly @EJ.

  But:

  As I understood, the default values have the a priori assumption that each model has an equal probability? Is this correct?

  Not really. How likely each model is to begin with is not specified here—that's a subjective belief and that's up to you. The Bayes Factor just tells you how much you should update your subjective belief given the data.

  To give an example: Say that, before you collected the data, you found it 20 × more likely that there is a valence × group interaction than that there isn't; but then you find that the inclusion BF for this interaction is 0.2. The rational thing to do would then be to multiply your initial belief by 0.2, which means that—despite the data—you still find it 4 times more likely that this interaction exists than that it does not. The idea is simple: If you're very convinced of something, you need strong evidence to change your mind.

  What the options in JASP do specify, in a way that I don't fully understand either, is which hypotheses you're comparing exactly: Notably, do you expect a large effect, or a small one? By default, JASP assumes that you're testing for a medium-size effect.

  3) Is it a valid approach to leave the values as they are and mention in my article that I used the default values or do I have to be afraid that some reviewers will to ask me what I mean by default values and why I did not change them?

  Other than a general fear that is justified during any review process, I don't think you have anything to be afraid of if you stick to the defaults.

  Cheers!
  Sebastiaan

  
  
  Check out SigmundAI.eu for our OpenSesame AI assistant!
  
• v.b

  April 2017 edited April 2017

  Hi Sebastiaan,

  thanks a lot for your answers.

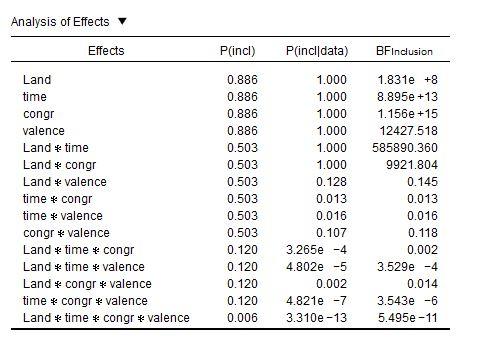
  I now calculated the ANOVA and ticked the effect box (see attached Picture). But now I`m a bit confused with the interpretation.

  If I get you and also Wagenmaker`s article (Bayesian Inference for Psychology. Part II: Example
  Applications with JASP) right, than it is ok, to report only the BFinclusion factors in an article. Especially when calculating with lots of factors (my model comparison table is huge). So, some more questions, I hope you can help me with.

  1) BFincl tells me how strongly the inclusion of one factor (averaged over all models that include that factor) is supported by the data compared to a nullmodell right?

  So, by looking at my table I`d say the the inclusion of

  • land (=Group)
  • time
  • congruency
  • valence
  • land * time
  • land * congruency

  is strongly supported?

  2) The bayesian results differ from the frequentistic ANOVA as land and congruency*land did not become significant there. I did not expect such discrepancy between those two approaches. And I`m not sure how to handle this, when interpreting the results-

  3) Is it valid to interpret BFincl factors like this:
  A model including the factor time is 1.8e+8 more likely than a model without this factor/a null Modell.

  Thanks again for your time and patience,
  VB
  
• sebastiaan

  April 2017

  1) BFincl tells me how strongly the inclusion of one factor (averaged over all models that include that factor) is supported by the data compared to a nullmodell right?

  Almost! But the comparison is not (only) with the null model, but with all other models.

  To illustrate: Say that you're investigating the probability of a light turning on (light) as a function of whether a broken light switch is flipped (switch), whether a butterfly short-circuits the electricity wires (butterfly), and the interaction (switch × butterfly).

  The full model would then be:

  light ~ switch + butterfly + switch × butterfly
  

  This full model, which includes the interaction, would perform much better than the null model. But that's simply because the main effect of butterfly is in there, and not because there is any evidence for the interaction—there's isn't because the light switch is broken, so it has no main effect nor does it interact with anything.

  The best model would be:

  light ~ butterfly
  

  Therefore, to quantify evidence for switch × butterfly, you should compare the model with the interaction (i.e. the full model) to all models without the interaction—and not just to the null model. And that's what the inclusion Bayes Factor does.

  (In this example there are only a few models, so you could in principle also compare them one by one. But in many cases, as in your case, that's not practical, and the inclusion Bayes Factor becomes indispensable.)

  So, by looking at my table I`d say the the inclusion of land (=Group), time, congruency, valence, land * time, land * congruency is strongly supported?

  Absolutely.

  The bayesian results differ from the frequentistic ANOVA as land and congruency*land did not become significant there. I did not expect such discrepancy between those two approaches. And I`m not sure how to handle this, when interpreting the results-

  That's odd. It's not uncommon for traditional ANOVA results to differ a bit from their bayesian counterparts, but—if so—it's usually the other way around: significant results show inconclusive bayes factors. Also, in your case, the inclusion BF is so massive that you would expect the result to be significant in a traditional analysis too. In general, your effects are very, very large.

  If you create an interaction plot for the congruency × land interaction (for example with land on the x axis and congruency as different lines), what does it look like?

  Perhaps it would be a good idea if you attach the JASP file here (with the data and the analyses), plus a brief description of what it all means. Then we can try to figure out what's happening here.

  Is it valid to interpret BFincl factors like this: A model including the factor time is 1.8e+8 more likely than a model without this factor/a null Modell.

  Bayesians prefer if you phrase things in terms of the likelihood of data given a hypothesis, rather than the other way around (although there is some fuzziness around this, and you'll find both descriptions in the wild; see for example this discussion). So you could say: the data are X times more likely under models that include factor Y than models that do not include factor Y.

  Personally, I would probably say something like: "The inclusion Bayes Factor for Y was X, indicating that there was [strong|substantial|...] evidence for Y." That seems pretty short and clear to me, and also reflects the analysis that you used.

  
  
  Check out SigmundAI.eu for our OpenSesame AI assistant!
  
• v.b

  April 2017

  I see. Thanks a lot for the example. This made it clear. A main effect of butterfly sounds like a start for an science fiction story, don`t you think? :-)

  I attached the results of the frequentistic ANOVA. Regarding the congruency x land intercation, even though it is not significant, there is at least a tendency, so maybe that is the reason for the high BF? But regarding the main effect of land that is not the case.
  Uploading the Jasp file is something I have to discuss with my co-authors first, as those are still unpublished data, which probably shouldn`t be publicly available for everyone.

  Bayesians prefer if you phrase things in terms of the likelihood of data given a hypothesis, rather than the other way around (although there is some fuzziness around this, and you'll find both descriptions in the wild; see for example this discussion).

  I read the discussion you suggested . Before reading that I thought bayesian factors are the probability that H0 is true given the data (and not the probability of the data given that H0 is true, which is what p-values are). Thus, I thought BFincl provides evidence for the H1 (compared to the H0) given the data and not the other way. Isn t this one of the main reasons to use bayesian statistics? To make statements regarding the probability of H0 or even say, that Ho is unlikely to be true (given the data) which we can`t do by just normal significance testing. But in the discussion and also in the way you phrased it (the data are X times more likely under models that include factor Y than models that do not include factor Y) it seems to be exactly the opposite (likelihood of the data given H0)?

  Thanks again!
• sebastiaan

  April 2017

  A main effect of butterfly sounds like a start for an science fiction story, don`t you think? :-)

  You would think so. I actually started writing a book about it; it had a cover and everything. But when developing it into a full-length story, I found that the theme is a bit limited after all. And also some trouble with my muse, etc. You know, writer's stuff. The book never finished.

  In any case, the story that your Bayes Factors are telling us is far more interesting. Let's take another look at your table:

  

  It's not just the Land × congr interaction: Also the main effect of Land is barely present in the traditional repeated measures, while it has an inclusion BF of 183 million in favor of it.

  Now note this: More than anything else, the inclusion BFs seem to indicate the complexity of the factors:

  • Main effects have a lot of evidence in favor—more evidence than a psychology experiment can realistically provide
  • Two-way interactions go either way
  • Three-way interactions have a lot of evidence against
  • And the four-way interaction, well, a lot of evidence against—again more evidence than a psychology experiment can realistically provide

  This got me thinking that this type of complexity gradient may be a general property of inclusion BFs. And they are—if you generate a random dataset with a lot of factors (like yours), you get a similar pattern:

  

  That is, the complex factors have far stronger evidence against them than the simple factors. However (and fortunately), no factors get evidence in favor of them—not with purely random data.

  But what I'm thinking now is that the inclusion BFs are biased. In your case, there is some very weak evidence for an effect of Land and also a Land × congr interaction—you can see this in the output of the traditional repeated measures. But when calculating the inclusion BFs, these weak tendencies seem to be amplified so that there seems to be overwhelming evidence in support for them.

  Or something like that. This goes way beyond my knowledge of Bayesian statistics.

  @EJ What do you make of this? Am I completely missing the concept of inclusion BFs? Something weird is going on here, right?

  
  
  Check out SigmundAI.eu for our OpenSesame AI assistant!
  
• EJ

  April 2017

  Well, this is interesting. Let me start by stressing that this is the result that probability theory gives us. So given the prior and the likelihood, these are the unique results. Our job here is to understand why it all makes sense (because probability theory ensures that it makes sense).

  In general, with many factors I do like to look at the inclusion table. However, I also would like to see the table with each model separately. In general, with respect to your simulation, random data do not support any of the models. In such a case the more complex models (i.e., those with interactions) will have stronger evidence going against them than simpler models. So that pattern makes sense. But I see that you have a later post that delves into the issue more deeply, so I'll look at that now.

  Cheers,
  E.J.