Interpreting complex bayesian repeated measures anova
Hi,
I am new you JASP and the use of Bayesian statistics, and i have trouble with the interpretation of my output.
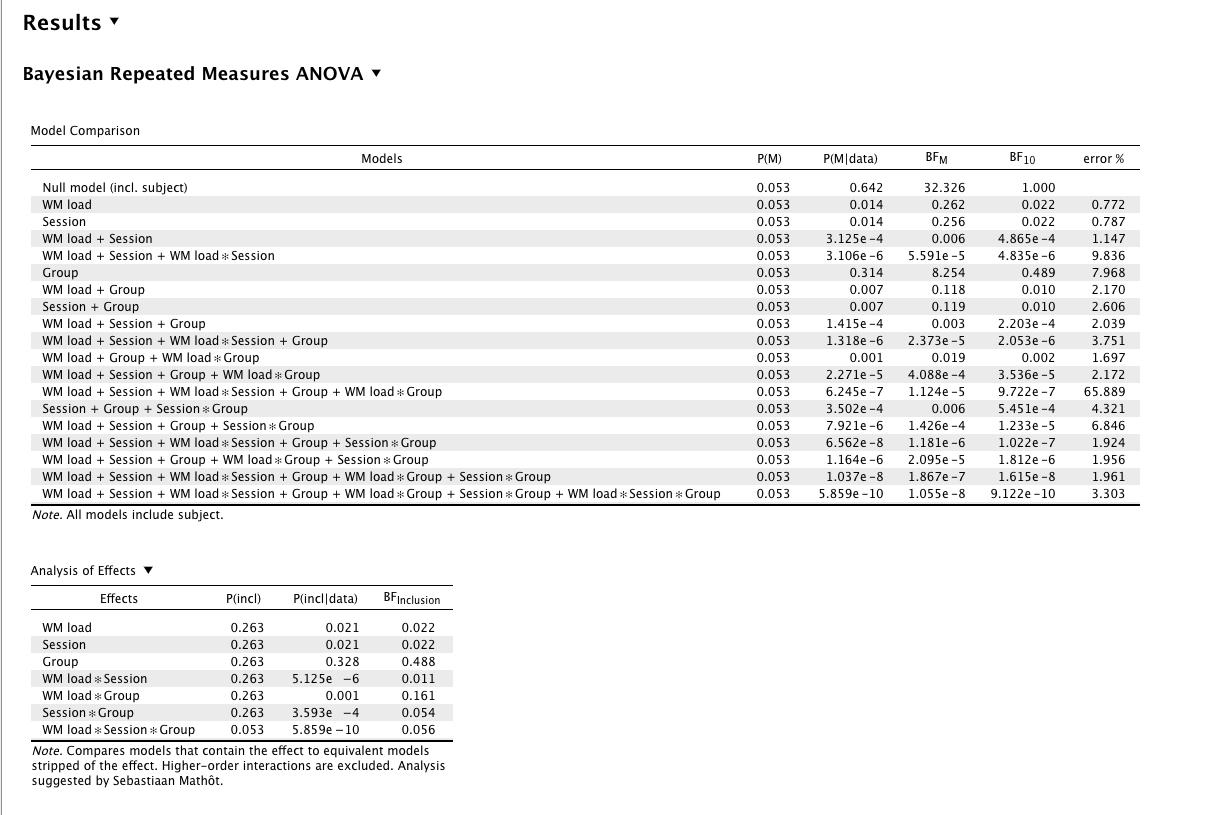
For the analysis i made use of a repeated measures anova with two factors (3 levels per factor). The analysis was for a working memory test with 3 levels (very low wm load, low wm load and high wm load). The participants did this task in 3 different sessions (2 weeks in between). The experimental condition was the difference between an active and placebo group.
My main interest is the difference between the groups. Does the active group get a higher or lower score in the working memory task than the placebo group?
As it is my first time using this method, i am unsure about how to interpret the effects (what value do i look at?) and how to report those.
In the literature i can only find examples of more easy tasks, but not of a complex analysis as this one.
Can you please help me?


Comments
Hi Joeri,
In your situation, I would focus on the second table, i.e. the inclusion Bayes ("Baws") Factor, and ignore the first table which (to me) is too overwhelming to be useful. Here is a blog in I describe the logic behind it. You can interpret the second table more-or-less as a regular RM Anova table, except that you have BF values instead of F and p values.
So:
Does that make sense? I would also create plot to help you interpret the effects, or lack thereof. You can do that also in JASP.
Hope this helps!
Cheers,
Sebastiaan
Check out SigmundAI.eu for our OpenSesame AI assistant!
@sebastiaan Thanks for the respons. This is really helpfull.
I've looked at your blog and that was pretty helpfull aswell. I have just one last question, i cant really find a source or an overview of when a Bfinclusion is evidence for or against an effect. Is there a sort of guideline for this? what do you use to base your conclusion upon?
For an intuitive idea of when a Bayes factor is compelling see
https://www.bayesianspectacles.org/lets-poke-a-pizza-a-new-cartoon-to-explain-the-strength-of-evidence-in-a-bayes-factor/
Cheers,
E.J.
Hi there,
Sorry to intrude into this thread but just to aid my own understand, you mentioned:
So:
Are the BFinclusion values based on the BF10 scale using the BF value 1 as the middle of the spectrum as adopted by JASP (refer link), or is it based on the traditional BF reading of <0.33 to <3? Because the BFinclusion values interpretation that you have made seems to be more consistent with the latter.
Link: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5991426/#CR23