Howdy, Stranger!

It looks like you're new here. If you want to get involved, click one of these buttons!

Sign In Register

Quick Links

Categories

Supported by

Bayes factor (inclusion BF) contradicts p value

gaspargaspar
edited September 2019 in JASP & BayesFactor

I'm running Repeated Measures ANOVAs on this data file: https://osf.io/3gynm/ (results_aggregated_exp2_index_vs_thumb.txt)

I include the factors "Type" (probe vs. irrelevant) and "Hand-position" (index vs. thumb), for the "duration RT mean" variable: "duration_RT_mean_probe_0", "duration_RT_mean_irrelevant_0", "duration_RT_mean_probe_1", "duration_RT_mean_irrelevant_1" (where _0 is index and _1 is thumb). See:

image.png


And what's weird is that for the interaction I find a p = .004:

image.png


But a BF = 0.182 (inclusion BF based on matched model - when based on all models, it's even 0.077):

image.png

So p value supports difference quite strongly (.004), and BF supports equivalence substantially (1 / 0.182 = 5.495). (There is a similar contradiction for the Type main effect too, but there at least the p value is not so clear.)

Any ideas what to make of this? Perhaps any references about interpreting such a case?

Comments

  • eniseg2eniseg2

    I've understood this analysis quite differently from you, so maybe someone can help both of us.

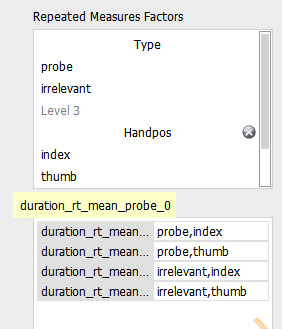
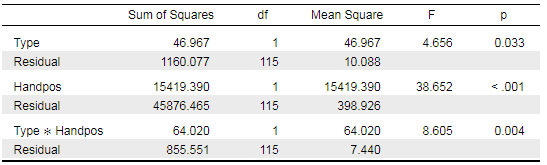
    My interpretation of your data would be as follows: when testing Type*Handpos against the null model, p=.004 suggests that there is only a 0.4% chance of data as extreme as yours or even more extreme than yours occurring, if the null model is true. So you reject the null model, you reject that there is no effect in your data. Therefore, you assume that there is an effect. To investigate which effect is most relevant or most "effective" in your data, you run your Bayesian analysis. I always run it set to BF01 and with the best model at the top. That makes selecting the model which best explains your data easy.

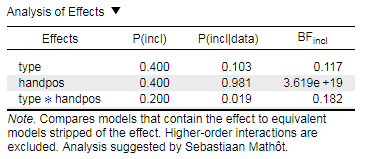
    Based on the analysis of effects which you have provided, I would conclude to only add handpos to the model and to exclude type as well as type*handpos. The model containing handpos on its own has a much higher BFincl than the other two. I hope I've got that right...

  • EJEJ

    Interesting case. Could you also provide the regular table with all the models separately? Maybe also a plot of the results?

    Sometimes such discrepancies are due to model misspecification, for instance heteroscedasticity etc.

    Cheers,

    E.J.

  • gaspargaspar
    edited September 2019

    @eniseg2: Thanks for the reply, but I'm not comparing against null, it's inclusion Bayes factors, which compares effects taking into account all effects. I'm no expert, but all in all I'm pretty sure it should generally give results that correspond to those from regular ANOVA.

    @EJ:

    Sure, here is the full table:

    image.png


    And here is a plot with 95% CI error bars:

    image.png

    (I know the probe vs. irrelevant difference looks tiny, but the correlation is super high [r(70) = .98], hence the significant difference.)

    Density plots:

    image.png

    Q-Q plot:

    image.png


    There are no between-subject factors, and the sphericity looks fine:

    image.png

    Again, the entire dataset is available at https://osf.io/3gynm/

    Btw, I actually ran these tests in R first, and only checked in JASP because of the strange results - but it's all the same. That's just to say that it's not something JASP-specific.

  • EJEJ

    Hmm I don't quite get this then. The discrepancy between the analyses is really large. I will ask some other people to look at this as well. Also, you could t-test just the probe vs irrelevant difference for the index case -- I assume your p-value will be even more significant, and the BF will be highly in favor of the alternative. Such a result would make the discrepancy even more mysterious.

    E.J.

  • EJEJ

    Update: if you present the R code, Richard can look with the BayesFactor package at what you did!

    Cheers,

    E.J.

  • gaspargaspar

    Yes, the probe-irrelevant difference in case of index:

    t(115) = –3.37, p = .001, d = –0.31, 95% CI [–0.50, –0.13], BF10 = 20.22.

    Correlation: r(114) = .979, 95% CI [.969, .985], p < .001.

    Descriptives: M±SD = 80.78±21.25 vs. 82.16±21.37


    In case of thumbs:

    t(115) = 0.29, p = .772, d = 0.03, 95% CI [–0.16, 0.21], BF01 = 9.31. (BFplain = 0.1074)

    Correlation: r(114) = .984, 95% CI [.977, .989], p < .001.

    Descriptives: M±SD = 93.05±22.28 vs. 92.95±22.30


    Here are the R codes along with a simplified dataset (with the relevant data only):


  • jcostajcosta
    edited October 2019

    @gaspar We've encountered the same issue with our data. Have you figured out how to interpret your findings?

  • gaspargaspar

    Nope, I wouldn't know how to. I'm still hoping @EJ or @richarddmorey might be able to explain it.

    (Fortunately this is not so important for me in this present data; this is just an additional and fairly unimportant exploratory analysis in our paper. Plus we originally reported it without BFs, I only checked this when it was already under review. Still it would be good to at least mention and clarify this in a footnote before publishing it.)

Sign In or Register to comment.
Sebastiaan Mathôt » v2.0.18 » Copyright 2011 — 2019 » Vanilla flavored » License

agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq, agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq , dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games