repeated measures Bayesian ANOVA example
Hi. I have conducted a standard repeated-measures ANOVA, where I found a significant main effect of trial difficulty, but (most interesting to me) no significant main effect of trial type, or significant interaction between trial type and trial difficulty.
I'd therefore like to supplement the p-values with Bayes factors (BF). Please can I check my interpretation of the Bayesian output below?
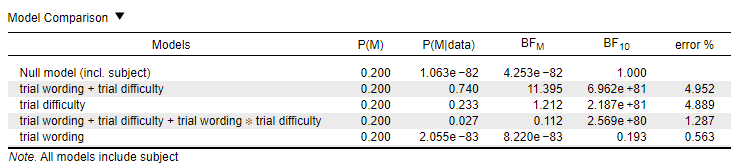
- For the significant main effect of trial difficulty: There was extreme evidence in favour of the alternative hypothesis (BF10 = 2.187 x 10^81, or for simplicity, BF10 > 100)
- For the non-significant main effect of trial wording: There was moderate evidence in favour of the null (BF10 = .193).
- For the non-significant interaction between difficulty and trial wording: There was strong evidence in favour of the null (BF10 = .037). This interaction estimate was calculated by calculating 2.569 x 10^80 / 6.962 x 10^81.
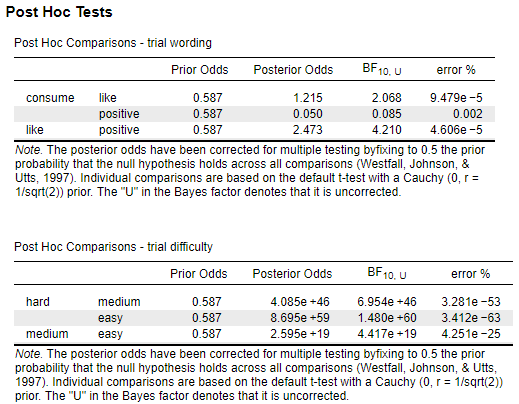
I wanted to ask one last thing relating to post-hoc tests. As I am specifically interested in the null, I have decided to report post-hoc tests with Bonferroni corrections for the main effects and interaction from the frequentist ANOVA. But how would I interpret, and report, these post-hoc comparisons from the Bayesian ANOVA?
It says the Bayes factor is uncorrected, but if I was transparent about this, would it make sense to report these? Or generally is it better practice to interpret and report the Posterior Odds which have been corrected using the Westfall et al. (1997) method. If I did report Posterior Odds:
- For trial wording, is it correct to interpret that there is strong support for the null between the consume and positive conditions (odds = .05), but inconclusive / anecdotal evidence for H1 for the other comparisons (odds 1.22 and 2.47)?
- For trial difficulty, there is extreme evidence to support the alternative hypothesis for all comparisons (all odds > 100)?
- Finally, is there is no option to compute post-hoc tests for the interaction?
Please let me know your thoughts, thank you!








Comments
Hi ABC_95,
Basically, "yes, this is correct" to all of the above. For the ANOVA table you might want to put the best model on top, as this usually makes the output easier to interpret.
Cheers,
E.J.