agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games








Comments
Hi Mateus,
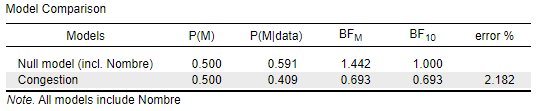
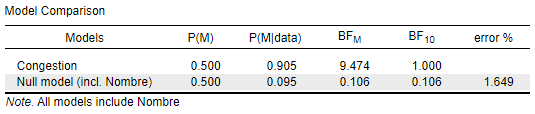
This happens because "compare to best model" is the default setting, and the first row gives the model of reference. The BF in the first row is always 1 because the model is compared to itself. In the first table there is a smidgen of evidence for H0 (you can also see this from the posterior model probabilities, P(M|data)). In the second table, there is evidence against H0 -- BF_10 = 0.106, meaning the data are 0.106 times more likely under whatever model is in the row (in this case H0) relative to the reference model (in this case the model with Congestion). The subscripts on the BF are confusing here and we intend to change those in the future. But you can see the direction of the evidence by looking at the P(M|data) column.
Cheers,
E.J.
Hi E.J.,
First of all, thank you for your response. Second, sorry to bother you again with news questions.
Can I make the following assumptions:
Table 1 - Anecdotal evidence for the null hypothesis in the accelerations variable was observed.
Table 2 - The Bayes factor indicates moderate evidence that the distance covered is not influenced by the competition period, as the data was 0.106 times more likely to occur under the null model.
Thank you in advance,
Mateus
Your conclusion for Table 2 should be the other way around. 0.106 under the null is 1/0.106 = 9.43 under the alternative. That this is support *against H0* and *in favor of H1* is also evident from the P(M|data) column.
E.J.
Of course, my mistake.
Correction: the Bayes factor indicates moderate evidence that the distance covered is influenced by the competition period, as the data was 9.43 times more likely to occur under the competition period model (null model: BF10 = 0.106, BF01 = 1/0.106 = 9.43).
I have some trouble analysing the posterior model probability column. Can you tell me if a similar table to this one is available (please see picture below) to improve the description of my results?
Thank you in advance,
Mateus
Hi Mateus,
There isn't, as far as I know. But most people find it relatively straightforward to interpret posterior probability. Actually, our "pizza plot" method works with posterior probabilities. See https://www.bayesianspectacles.org/lets-poke-a-pizza-a-new-cartoon-to-explain-the-strength-of-evidence-in-a-bayes-factor/
E.J.
Hi E.J.,
Now I get it.
Thank you for your time,
Mateus
Now I get it.
Thanks a lot
______________________________________
air max 270 billigste