agen judi bola , sportbook, casino, togel, number game, singapore, tangkas, basket, slot, poker, dominoqq,
agen bola. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 50.000 ,- bonus cashback hingga 10% , diskon togel hingga 66% bisa bermain di android dan IOS kapanpun dan dimana pun. poker , bandarq , aduq, domino qq ,
dominobet. Semua permainan bisa dimainkan hanya dengan 1 ID. minimal deposit 10.000 ,- bonus turnover 0.5% dan bonus referral 20%. Bonus - bonus yang dihadirkan bisa terbilang cukup tinggi dan memuaskan, anda hanya perlu memasang pada situs yang memberikan bursa pasaran terbaik yaitu
http://45.77.173.118/ Bola168. Situs penyedia segala jenis permainan poker online kini semakin banyak ditemukan di Internet, salah satunya TahunQQ merupakan situs Agen Judi Domino66 Dan
BandarQ Terpercaya yang mampu memberikan banyak provit bagi bettornya. Permainan Yang Di Sediakan Dewi365 Juga sangat banyak Dan menarik dan Peluang untuk memenangkan Taruhan Judi online ini juga sangat mudah . Mainkan Segera Taruhan Sportbook anda bersama
Agen Judi Bola Bersama Dewi365 Kemenangan Anda Berapa pun akan Terbayarkan. Tersedia 9 macam permainan seru yang bisa kamu mainkan hanya di dalam 1 ID saja. Permainan seru yang tersedia seperti Poker, Domino QQ Dan juga
BandarQ Online. Semuanya tersedia lengkap hanya di ABGQQ. Situs ABGQQ sangat mudah dimenangkan, kamu juga akan mendapatkan mega bonus dan setiap pemain berhak mendapatkan cashback mingguan. ABGQQ juga telah diakui sebagai
Bandar Domino Online yang menjamin sistem FAIR PLAY disetiap permainan yang bisa dimainkan dengan deposit minimal hanya Rp.25.000. DEWI365 adalah
Bandar Judi Bola Terpercaya & resmi dan terpercaya di indonesia. Situs judi bola ini menyediakan fasilitas bagi anda untuk dapat bermain memainkan permainan judi bola. Didalam situs ini memiliki berbagai permainan taruhan bola terlengkap seperti Sbobet, yang membuat DEWI365 menjadi situs judi bola terbaik dan terpercaya di Indonesia. Tentunya sebagai situs yang bertugas sebagai
Bandar Poker Online pastinya akan berusaha untuk menjaga semua informasi dan keamanan yang terdapat di POKERQQ13. Kotakqq adalah situs
Judi Poker Online Terpercayayang menyediakan 9 jenis permainan sakong online, dominoqq, domino99, bandarq, bandar ceme, aduq, poker online, bandar poker, balak66, perang baccarat, dan capsa susun. Dengan minimal deposit withdraw 15.000 Anda sudah bisa memainkan semua permaina pkv games di situs kami. Jackpot besar,Win rate tinggi, Fair play, PKV Games








Comments
Hi Sofia,
that's a good question. Unfortunately, I also don't have a perfect answer here. One possible alternative to log transformation could be a square-root transformation as this can handle 0s.
However, values of exactly 0 for sample entropy should actually be unlikely to occur in practice (close to 0 might be possible, but exactly 0 could be an indicator that a trial has maybe only very few recorded positions, e.g., just start and end), so it might be worth inspecting those cases.
Best,
Pascal
Dear Pascal,
Thank you for your answer.
Actually, there are a lot of zero values of sample entropy and the mean is also very close to 0 (~0,06, maximum value: ~0.8), even though we have only kept trials that have more than 2 logged positions, and have also removed trials where the startpoint of the (time-normalised) trajectory appeared equal to the endpoint. Do you have any idea why that might be?
Best,
Sofia
Dear Sofia,
hmm I am not sure. Have you plotted the trajectories with sample entropy values of 0 to check?
Best,
Pascal
Dear Pascal,
Thanks a lot for your suggestions.
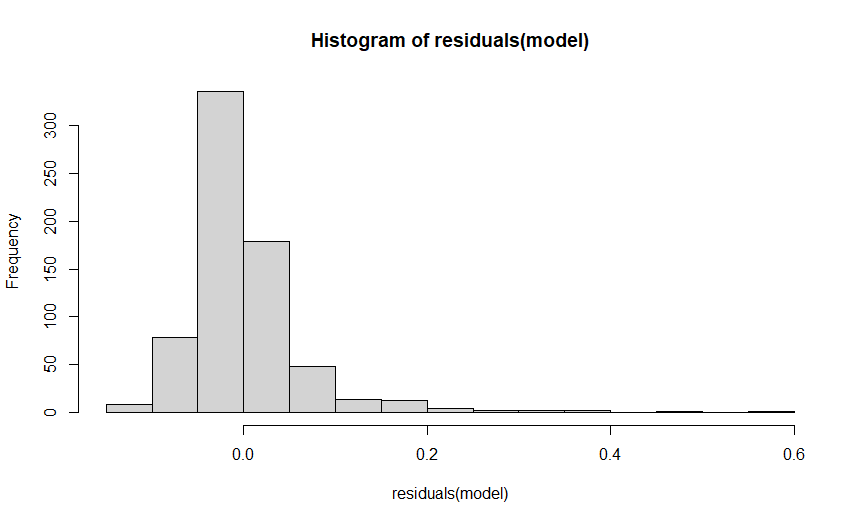
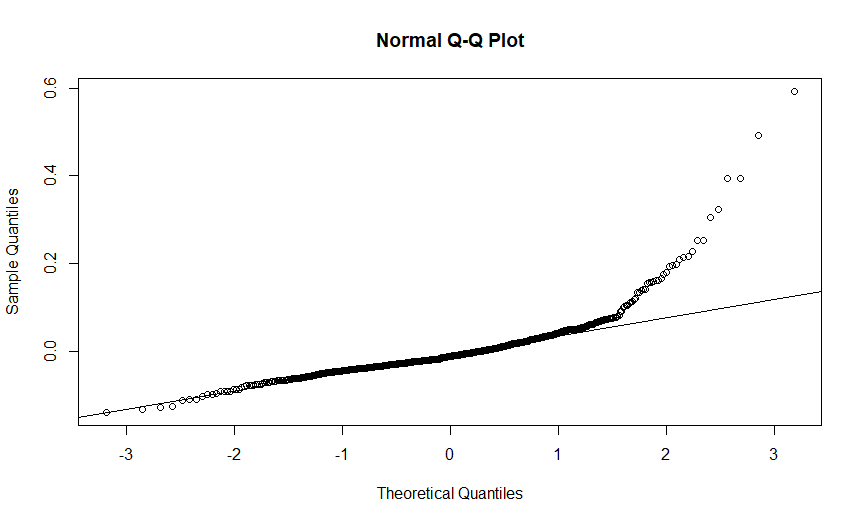
I transformed sample entropy with square root transformation and this seems to normalise the distribution a bit and improve the residuals (see residual plot of model with transformed entropy below).
As for the zero values of entropy, I plotted the trajectories for those specific trials as you suggested and they are indeed very small in size, which I guess results in the zero values (compare overall trajectories and trajectories with entropy=0 in plots below). However, I would be hesitant to delete them as they are still informative. Also, as I mentioned before, the positive values of entropy are still very small and close to zero. We suspect it could be due to the small size of the time interval we are investigating (time normalised to 101 steps). Note that we don't look at the whole mouse trajectory (starting from 0,0) but part of it, that's why trajectories appear to start further up.
Would you possibly have time to take a look at our design? It is more complicated than previous mousetracking studies (e.g. Freeman & Ambady 2010) and so we might miss something still..
Thanks again for your time!
Sofia
Dear Sofia,
please excuse the delayed reply. As I have left academia some time ago (transitioning into an industry position), it usually takes me some time to answer questions in the forum as I can only check it in my free time. (I still continue to maintain the open source packages I developed, e.g., mousetrap, and I am also happy to provide support through this forum.)
I think that based on what you wrote and what can be seen in the plots it is quite plausible that you have sample entropy values close to zero as you are only looking at very short and, more importantly, mostly straight trajectory with little fluctuation. The only solution I could imagine is to look at a greater parts of the trajectories (if I understood you correctly you only look at trajectory parts in your analysis).
Best,
Pascal